Giải bài tập Bài 3 trang 89 Toán 8 Tập 2 | Toán 8 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 3 trang 89 Toán 8 Tập 2. Bài 9. Hình đồng dạng.. Toán 8 - Cánh diều
Đề bài:
Bài 3 trang 89 Toán 8 Tập 2: Cho hai hình chữ nhật ABCD và A’B’C’D’ có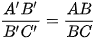 
Trên các tia AB, AC, AD ta lần lượt lấy các điểm B’’, C’’, D’’sao cho 
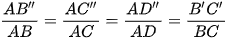. Chứng minh:
a) Hình chữ nhật AB’’C’’D’’ đồng dạng phối cảnh với hình chữ nhật ABCD;
b) AB’’ = A’B’, B’’C’’ = B’C’;
c) Hai hình chữ nhật ABCD và A’B’C’D’ là đồng dạng.
Đáp án và cách giải chi tiết:
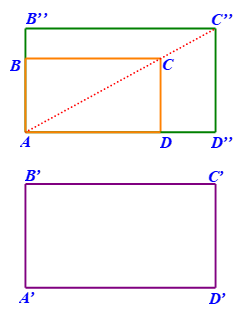
a) Ba đường thẳng AB’’, AC’’, AD’’ cùng đi qua điểm A và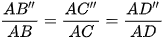 
nên hai hình chữ nhật A’’B’’C’’D’’ và ABCD là đồng dạng phối cảnh và điểm A là tâm đồng dạng phối cảnh.
b) Hai hình chữ nhật ABCD và A’B’C’D’ có 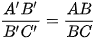nên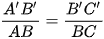 
Mà 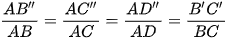(giả thiết) và 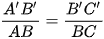(do A’’B’’C’’D’’ và ABCD là đồng dạng phối cảnh)
Suy ra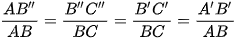 
Do đó AB’’ = A’B’, B’’C’’ = B’C’.
c) Hai hình chữ nhật A’’B’’C’’D’’ và A’B’C’D’ có: AB’’ = A’B’, B’’C’’ = B’C’ nên hai hình chữ nhật A’B’C’D’ và A’’B’’C’’D’’ bằng nhau.
Mà hình chữ nhật A’’B’’C’’D’’ đồng dạng phối cảnh với hình chữ nhật ABCD.
Vậy hai hình chữ nhật ABCD và A’B’C’D’ là đồng dạng.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 86 Toán 8 Tập 2
Khởi động trang 86 Toán 8 Tập 2: Hình 90 mô tả hai bức ảnh cùng chụp Ngọ Môn (Hoàng Thành Huế) nhưng có kích thước khác nhau:
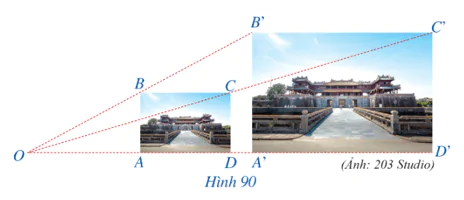
Hai bức ảnh trong Hình 90 giống hệt nhau nhưng có kích thước to nhỏ khác nhau gợi nên những hình có mối liên hệ gì?
Hoạt động 1 trang 86 Toán 8 Tập 2
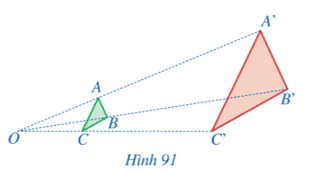
Hoạt động 1 trang 86 Toán 8 Tập 2: Cho hai tam giác ABC và A’B’C’ sao cho ba đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và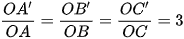 
(Hình 91). Tam giác A’B’C’ nhận được từ tam giác ABC bằng cách nào?
Hoạt động 2 trang 86 Toán 8 Tập 2
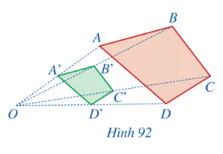
Hoạt động 2 trang 86 Toán 8 Tập 2: Cho hai tứ giác ABCD và A’B’C’D’ sao cho bốn đường thẳng AA’, BB’, CC’, DD’ cùng đi qua điểm O và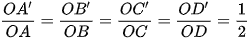 
(Hình 92). Tứ giác A’B’C’D’ có thể nhận được từ tứ giác ABCD bằng cách nào?
Hoạt động 3 trang 87 Toán 8 Tập 2
Hoạt động 3 trang 87 Toán 8 Tập 2: Thực hiện các hoạt động sau.
a) Cắt ra từ tờ giấy kẻ ô vuông:
– Hình chữ nhật ABCD có AB = 3 cm, AD = 2 cm; hình chữ nhật A’B’C’D’ có A’B’ = 3 cm, A’D’ = 2 cm;
– Hình vuông MNPQ có MN = 4 cm; hình vuông M’N’P’Q’ có M’N’ = 4 cm.
b) – Đặt hai mảnh giấy hình chữ nhật ABCD và A’B’C’D’ "chồng khít" lên nhau.
– Đặt hai mảnh giấy hình vuông MNPQ và M’N’P’Q’ "chồng khít" lên nhau.
Hoạt động 4 trang 88 Toán 8 Tập 2
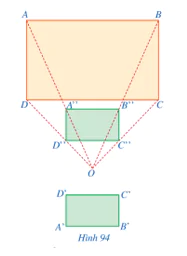
Hoạt động 4 trang 88 Toán 8 Tập 2: Trong Hình 94, hình chữ nhật ABCD có AB = 9 cm, AD = 6 cm; hình chữ nhật A’B’C’D’ có A’B’ = 3 cm, A’D’ = 2 cm; hình chữ nhật A’’B’’C’’D’’ có A’’B’’ = 3 cm, A’’D’’ = 2 cm. Quan sát Hình 94 và cho biết:
a) Hai hình chữ nhật A’’B’’C’’D’’, ABCD có đồng dạng phối cảnh hay không.
b) Hai hình chữ nhật A’B’C’D’, A’’B’’C’’D’’ có bằng nhau hay không.
Bài 1 trang 89 Toán 8 Tập 2
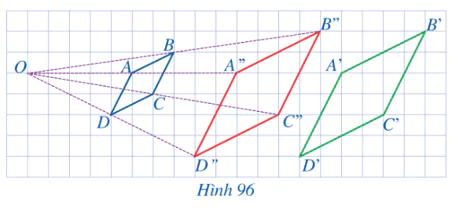
Bài 1 trang 89 Toán 8 Tập 2: Trong Hình 96, các điểm A, B, C, D lần lượt là trung điểm của các đoạn thẳng OA’’, OB’’, OC’’, OD’’. Quan sát Hình 96 và cho biết:
a) Hai hình thoi A’B’C’D’ và A’’B’’C’’D’’có bằng nhau hay không;
b) Hai hình thoi A’B’C’D’ và ABCD có đồng dạng hay không.
Bài 2 trang 89 Toán 8 Tập 2
Bài 2 trang 89 Toán 8 Tập 2: Cho tam giác ABC có AB = 3, BC = 6, CA = 5. Cho O, I là hai điểm phân biệt.
a) Giả sử tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với điểm O là tâm đồng dạng phối cảnh, tỉ số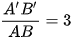 
.
Hãy tìm độ dài các cạnh của tam giác A’B’C’.
b) Giả sử tam giác A’’B’’C’’ là hình đồng dạng phối cảnh của tam giác ABC với điểm I là tâm đồng dạng phối cảnh, tỉ số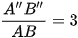 
. Hãy tìm độ dài các cạnh của tam giác A’’B’’C’’.
c) Chứng minh ∆A’B’C’ = ∆A’’B’’C’’.
Chú ý: Hai tam giac cùng là hình đồng dạng phối cảnh tỉ số k (tâm đồng dạng phối cảnh có thể khác nhau) của một tam giác luôn bằng nhau.