Giải bài tập Toán 12 Bài tập cuối chương 2 | Chân trời sáng tạo
Hướng dẫn giải chi tiết SBT Bài tập cuối chương 2
Bài 1 trang 77 SBT Toán 12 Tập 1
Cho hai điểm A(1; 1; −2) và B(2; 2; 1). Tọa độ của vectơ là
A. (3; 3; −1).
B. (−1; −1; −3).
C. (3; 1; 1).
D. (1; 1; 3).
Bài 2 trang 77 SBT Toán 12 Tập 1
Cho hai vectơ = (1; 2; −3) và = (−2; −4; 6). Trong các khẳng định sau, khẳng định nào đúng?
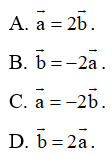
Bài 3 trang 77 SBT Toán 12 Tập 1
Cho hai điểm A(2; 0; 1) và B(0; 5; −1). Tích vô hướng của hai vectơ và bằng
A. −2.
B. −1.
C. 1.
D. 2.
Bài 4 trang 77 SBT Toán 12 Tập 1
Cho hai vectơ thỏa mãn . Tọa độ của vectơ là
A. (2; 1; −3).
B. (2; −3; 1).
C. (1; 2; −3).
D. (1; −3; 2).
Bài 5 trang 77 SBT Toán 12 Tập 1
Cho ba vectơ = (−1; 1; 0), = (1; 1; 0) và = (1; 1; 1). Trong các khẳng định sau, khẳng định nào sai?

Bài 6 trang 77 SBT Toán 12 Tập 1
Cho hai vectơ = (−3; 4; 0) và = (5; 0; 12). Côsin của góc giữa hai vectơ và bằng

Bài 7 trang 77 SBT Toán 12 Tập 1
Góc giữa hai vectơ và bằng
A. 30°.
B. 60°.
C. 120°.
D. 150°.
Bài 8 trang 77 SBT Toán 12 Tập 1
Hai vectơ = (m; 2; 3) và = (1; n; 2) cùng phương khi

Bài 9 trang 78 SBT Toán 12 Tập 1
Cho hai vectơ = (2; 1; −2) và = (0; 2m; −4). Giá trị của tham số m để hai vectơ và vuông góc với nhau là
A. m = −4.
B. m = −2.
C. m = 2.
D. m = 4.
Bài 10 trang 78 SBT Toán 12 Tập 1
Cho hai điểm A(2; 3; −1) và B(0; −1; 1). Trung điểm I của đoạn thẳng AB có tọa độ là
A. (1; 1; 0).
B. (2; 2; 0).
C. (−2; −4; 2).
D. (−1; −2; 1).
Bài 11 trang 78 SBT Toán 12 Tập 1
Cho hai vectơ = (1; 1; −2), = (−3; 0; −1) và điểm A(0; 2; 1). Tọa độ điểm M thỏa mãn là
A. M(−5; 1; 2).
B. M(3; −2; 1).
C. M(1; 4; −2).
D. M(5; 4; −2).
Bài 12 trang 78 SBT Toán 12 Tập 1
Cho điểm A(3; −1; 1). Hình chiếu vuông góc với điểm A trên mặt phẳng (Oyz) là điểm
A. M(3; 0; 0).
B. N(0; −1; 1).
C. P(0; −1; 0).
D. Q(0; 0; 1).
Bài 13 trang 78 SBT Toán 12 Tập 1
Cho điểm M(−3; 2; −1) và điểm M' là điểm đối xứng với M qua mặt phẳng (Oxy). Tọa độ điểm M' là
A. (−3; 2; 1).
B. (3; 2; 1).
C. (3; 2; −1).
D. (3; −2; −1).
Bài 14 trang 78 SBT Toán 12 Tập 1
Hình chiếu vuông góc của điểm M(2; 1; −1) trên trục Oz có tọa độ là
A. (2; 1; 0).
B. (0; 0; −1).
C. (2; 0; 0).
D. (0; 1; 0).
Bài 15 trang 78 SBT Toán 12 Tập 1
Cho điểm A(−3; 1; 2) và điểm A' là điểm đối xứng của A qua trục Oy. Tọa độ của điểm A' là
A. (3; −1; −2).
B. (3; −1; 2).
C. (3; 1; −2).
D. (−3; −1; 2).
Bài 16 trang 78 SBT Toán 12 Tập 1
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2.
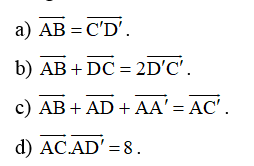
Bài 17 trang 79 SBT Toán 12 Tập 1
Cho hai điểm A(3; −2; 4), B(5; 0; 7).
a) .
b) = (8; −2; 11).
c) Điểm B nằm trong mặt phẳng (Oxz).
d) 2 = (10; 0; 14).
Bài 18 trang 79 SBT Toán 12 Tập 1
Cho hai vectơ = (2; 1; 5) và = (5; 0; −2).
a) .
b) cùng phương.
c) = (7; 1; 3).
d) = 1.
Bài 19 trang 79 SBT Toán 12 Tập 1
Cho một lực = (4; 6; 9) (đơn vị: N) thực hiện một độ dịch chuyển = (20; 50; 10) (đơn vị: m).
a) Cường độ của lực là N.
b) Độ dài quãng đường dịch chuyển là m.
c) Công sinh bởi lực khi thực hiện độ dời là J.
d) .
Bài 20 trang 79 SBT Toán 12 Tập 1
Hai vật đang chuyển động với vận tốc lần lượt là = (2; 1; 5) và = (8; 4; 20).
a) Hai vật đang chuyển động cùng hướng.
b) = 120.
c) cos = 1.
d) cos = 0.
Bài 1 trang 79 SBT Toán 12 Tập 1
Cho hai vectơ = (0; 1; 3) và = (−2; 3; 1). Tìm tọa độ vectơ thỏa mãn .
Bài 2 trang 80 SBT Toán 12 Tập 1
Cho ba vectơ = (1; 0; −2), = (−2; 1; 3) và = (−4; 3; 5). Tìm hai số thực m, n sao cho .
Bài 3 trang 80 SBT Toán 12 Tập 1
Cho hai vectơ = (2; m + 1; −1) và = (1; −3; 2). Tìm giá trị nguyên của m để .
Bài 4 trang 80 SBT Toán 12 Tập 1
Cho hai vectơ = (m; −2; m + 1) và = (0; m – 2; 1). Tìm giá trị của m, để hai vectơ và cùng phương.
Bài 5 trang 80 SBT Toán 12 Tập 1
Cho ba điểm A(2; −1; 3), B(−10; 5; 3) và M(2m – 1; 2; n + 2). Tìm m, n để A, B, M thẳng hàng.
Bài 6 trang 80 SBT Toán 12 Tập 1
Cho hai vectơ và thỏa mãn = 30°. Tính độ dài của vectơ .
Bài 7 trang 80 SBT Toán 12 Tập 1
Cho hai vectơ = (2; −1; 2), thỏa mãn . Tính độ dài của vectơ .
Bài 8 trang 80 SBT Toán 12 Tập 1
Cho hai vectơ thỏa mãn = 2, = 1 và = 60°. Tính góc giữa hai vectơ và .
Bài 9 trang 80 SBT Toán 12 Tập 1
Cho ba điểm A(−3; 4; 2), B(−5; 6; 2) và C(−4; 7; −1). Tìm tọa độ điểm D thỏa mãn .
Bài 10 trang 80 SBT Toán 12 Tập 1
Cho các điểm A, B, C có tọa độ thỏa mãn . Tìm tọa độ điểm D để tứ giác ABCD là hình bình hành.
Bài 11 trang 80 SBT Toán 12 Tập 1
Cho tam giác ABC có A(0; 0; 1), B(−1; −2; 0), C(2; 1; −1). Tìm tọa độ chân đường cao H hạ từ A xuống BC.
Bài 12 trang 80 SBT Toán 12 Tập 1
Cho sáu điểm A(1; 2; 3), B(2; −1; 1), C(3; 3; −3) và A', B', C' thỏa mãn . Tìm tọa độ trọng tâm G của tam giác A'B'C'.
Bài 13 trang 80 SBT Toán 12 Tập 1
Cho tam giác ABC có đỉnh C(−2; 2; 2) và trọng tâm G(−1; 1; 2). Tìm tọa độ các đỉnh A, B của tam giác ABC, biết điểm A thuộc mặt phẳng (Oxy) và điểm B thuộc Oz.
Bài 14 trang 80 SBT Toán 12 Tập 1
Cho ba điểm A(2; −1; 3), B(4; 0; 1) và C(−10; 5; 30). Đường phân giác trong của góc B của tam giác ABC cắt BC tại D. Tính BD.
Bài 15 trang 81 SBT Toán 12 Tập 1
Cho ba điểm A(1; 1;1 ), B(−1; 1; 0) và C(3; 1; −1). Gọi M(a; b; c) là điểm thuộc mặt phẳng (Oxz) và cách đều ba điểm A, B, C. Tính tổng a + b + c.
Bài 16 trang 81 SBT Toán 12 Tập 1
Trong không gian Oxyz được thiết lập tại một sân bay, người ta ghi nhận hai máy bay đang bay đến với các vectơ vận tốc = (90; −80; −120), = (60; −50; −60).

Tính góc giữa hai vectơ vận tốc nói trên (kết quả làm tròn đến hàng phần mười của độ).
Bài 17 trang 81 SBT Toán 12 Tập 1
Để nghiên cứu mô hình mạng tinh thể than chì, một nhà hóa học đã thiết lập một hệ tọa độ Oxyz như Hình 2 (đơn vị: nm). Cho biết ABCDEF có dạng lục giác đều.

Tìm tọa độ các điểm A, B, C, E, A'.
Bài 18 trang 81 SBT Toán 12 Tập 1
Một robot cắt dây đã di chuyển một lực = (0; 0; −150) (đơn vị: N) theo độ dời = (0; −8; −10) (đơn vị: m). Tính công sinh bởi lực khi thực hiện độ dời nói trên.
