Giải bài tập Toán 12 Bài tập cuối chương 1 | Chân trời sáng tạo

Hàm số y = f(x) trong Hình 1 nghịch biến trên khoảng nào?

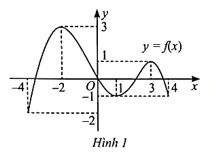
A. (−2; 1).

B. (−4; −2).

C. (−1; 3).

D. (1; 3).

Hàm số y = f(x) trong Hình 1 có bao nhiêu điểm cực trị?

A. 2.

B. 3.

C. 4.

D. 5.

Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [0; 4] trong Hình 1 là:

A. −1.

B. −2.

C. 0.

D. 1.

Cho hàm số y = $\frac{{\mathrm{x}}^2-2\mathrm{x}+1}{\mathrm{x}-2}$. Khi đó,

A. Hàm số đồng biến trên các khoảng (−∞; 1) và (3; +∞).

B. Hàm số đồng biến trên các khoảng (−1; 2) và (2; 3).

C. hàm số đồng biến trên khoảng (−∞; 2).

D. Hàm số đồng biến trên (2; +∞).

Cho hàm số y = x³ + 4x² – 3x + 4. Khi đó:

A. Hàm số đạt cực đại tại x = $\frac{1}{3}$, giá trị cực đại là $\frac{94}{27}$.

B. Hàm số đạt cực đại tại x = −3, giá trị cực đại là 22.

C. Hàm số đạt cực đại tại x = 0, giá trị cực đại là 4.

D. Hàm số không có cực đại.

Đồ thị đạo hàm f'(x) của hàm số y = f(x) được cho trong Hình 2.

Điểm cực tiểu của hàm số y = f(x) là:

A. x = −3.

B. x = −1.

C. x = 0.

D. x = 1.

Đồ thị đạo hàm f'(x) của hàm số y = f(x) được cho trong Hình 3.

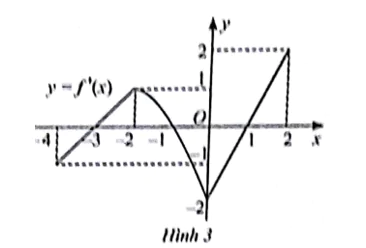
Hàm số y = f(x) đồng biến trên các khoảng

A. (−4; −2) và (−2; 2).

B. (−2; 0).

C. (−4; −3) và (−1; 1).

D. (−3; −1) và (1; 2).

Cho hàm số y = x³ – 12x + 6. Giá trị lớn nhất của hàm số trên đoạn [−3; 3] là

A. 6.

B. 15.

C. 17.

D. 22.

Cho hàm số y = $\frac{{\mathrm{x}}^2-2\mathrm{x}+6}{\mathrm{x}+1}$.

A. Đồ thị hàm số có một tiệm cận xiên là y = x – 3.

B. Đồ thị hàm số có một tiệm cận xiên là y = x + 3.

C. Đồ thị hàm số có một tiệm cận xiên là y = x +1.

D. Đồ thị hàm số không có tiệm cận xiên.

Đồ thị hàm số y = $\frac{-4\mathrm{x}+3}{2\mathrm{x}+2}$ có tâm đối xứng là điểm:

A. (−1; −2).

B. (−2; −1).

C. (−1; −1).

D. (−2; −2).

Cho hàm số y = 2x³ – 5x² – 24x – 18.

a) Hàm số có hai cực trị.

b) Hàm số đạt cực đại tại x = $-\frac{4}{3}$, giá trị cực đại là $\frac{10}{27}$.

c) Hàm số đồng biến trên khoảng (3; +∞).

d) Hàm số đồng biến trên khoảng $(-\frac{4}{3}; 3)$.

Hàm số y = $\frac{3\mathrm{x}+1}{\mathrm{x}-2}$ có các tiệm cận là

a) x = 2.

b) x = 3.

c) y = 2.

d) y = 3.

Lợi nhuận một xưởng thu được từ việc sản xuất một mặt hàng được cho bởi công thức P(q) = −q³ + 24q² + 780q – 5000 (nghìn đồng) trong đó q (kg) là khối lượng sản xuất được. Xưởng chỉ sản xuất được tối đa 50 kg sản phẩm trong một tuần.

a) Xưởng sản xuất càng nhiều thì lợi nhuận càng cao.

b) Lợi nhuận lớn nhất khi xưởng sản xuất 26 kg sản phẩm trong một tuần.

c) Sau khi sản xuất được 26 kg sản phẩm, càng sản xuất thêm thì lợi nhuận càng giảm.

d) Lợi nhuận của xưởng thấp nhất khi không sản xuất.

Đồ thị hàm số y = $\frac{{\mathrm{x}}^2-2\mathrm{x}}{\mathrm{x}+1}$ có hai trục đối xứng là hai đường phân giác của các góc tạo bởi hai đường thẳng:

a) x = 1 và y = x – 3.

b) x = 1 và y = −x + 3.

c) x = −1 và y = x – 3.

d) x = −1 và y = x + 3.

Giá thành của một sản phẩm trong 6 tháng đầu năm thay đổi theo công thức P(t) = 2t³ – 33t² + 168t + 137 với P tính bằng nghìn đồng và t là số tháng tính từ đầu năm. Trong khoảng thời gian nào thì giá của sản phẩm tăng?

Người ta muốn làm một chiếc hộp hình hộp chữ nhật có đáy hình vuông và thể tích là 10 l. Diện tích toàn phần nhỏ nhất của hộp là bao nhiêu?

Cho hàm số y = f(x) = $\frac{\mathrm{m}+2}{3}$x³ + 2x² + (m + 2)x + 1 (m là tham số). Tìm m để đồ thị hàm số không có cực trị.

Tìm tọa độ tâm đối xứng I của đồ thị hàm số sau theo tham số m: y = f(x) = (2 – m)x³ – 3x² + 2. Chứng tỏ rằng khi m thay đổi, I luôn thuộc một parabol xác định.

Cho hàm số y = f(x) = $\frac{{\mathrm{x}}^2+2\mathrm{x}-\mathrm{m}}{\mathrm{x}-1}$ (m là tham số). Tìm m để đồ thị hàm số đã cho có hai cực trị.

Nam dùng một tấm bìa có kích thước 50 cm x 20 cm để làm một chiếc lon hình trụ (không có nắp).

Hỏi cần chọn bán kính đáy hình trụ là bao nhiêu xăng-ti-mét thì lon hình trụ đạt thể tích lớn nhất?

Lưu ý: Kết quả làm tròn đến hàng phần trăm của xăngtimét, bỏ qua phần hao hụt khi cắt và tạo hình, đáy và mặt bên phải là các bìa nguyên vẹn (không ghép nối).

Một chủ nhà hàng kinh doanh phần ăn uống đồng giá có chiến lược kinh doanh như sau:

● Phí cố định được ước tính trong một năm là 50 000 nghìn đồng.

● Chi phí một phần ăn ước tính khoảng 22 nghìn đồng.

● Giá niêm yết trên thực đơn là 30 nghìn đồng.

Trong bài này, giả định rằng tất cả các phần ăn chế biến sẵn đều được bán hết và kí hiệu x là số phần ăn tự phục vụ trong một năm, giả sử x thuộc khoảng [5000; 25 000].

a) Gọi C(x) là tổng chi phí hằng năm cho x phần ăn này. Xác định C(x).

b) Chứng tỏ rằng giá thành của một phần ăn cho bởi biểu thức D(x) = 22 + $\frac{50 000}{\mathrm{x}}$ (nghìn đồng).

c) Sử dụng đồ thị, hãy xác định điểm hòa vốn của nhà hàng, tức là số lượng phần ăn tối thiểu phải được phục vụ hằng năm để hoạt động của nhà hàng tạo ra lợi nhuận. Hãy chứng minh điều đó.

d) Chứng minh rằng tổng lợi nhuận hằng năm cho x phần ăn được biểu thị bởi:

L(x) = 8x – 50 000 (nghìn đồng).

e) Mục tiêu của chủ nhà hàng là tạo ra lợi nhuận ít nhất là 120 000 nghìn đồng mỗi năm. Biết rằng nhà hàng mở cửa 300 ngày một năm, hỏi trung bình mỗi ngày nhà phàng phải phục vụ ít nhất bao nhiêu phần ăn để đạt được mục tiêu trên.

Người ta muốn chế tạo một chiếc hộp hình chữ nhật có thể tích 800 cm³ với yêu cầu dùng ít vật liệu nhất.

Chiều cao hộp là 8 cm, các kích thước khác là x (cm), y (cm) với x > 0 và y > 0.

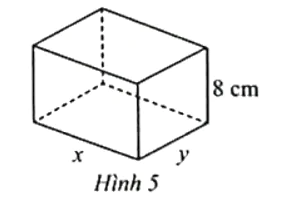
a) Chứng tỏ rằng y = $\frac{100}{\mathrm{x}}$.

b) Tìm diện tích toàn phần S(x) của chiếc hộp theo x.

c) Khảo sát hàm số S(x) trên khoảng (0; +∞).

d) Tìm kích thước của hộp để tiết kiệm vật liệu nhất. (Làm tròn kết quả đến hàng đơn vị của mi-li-mét).