Giải bài tập Luyện tập 2 trang 13 Toán 8 Tập 1 | Toán 8 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Luyện tập 2 trang 13 Toán 8 Tập 1. Bài 2. Các phép tính với đa thức nhiều biến. Toán 8 - Cánh diều
Đề bài:
Luyện tập 2 trang 13 Toán 8 Tập 1: Với ba đa thức A, B, C trong Ví dụ 3, hãy tính:
a) B – C;
b) (B – C) + A.
Đáp án và cách giải chi tiết:
Trong Ví dụ 3 có các đa thức: A = x2 – 2xy + y2; B = 2x2 – y2; C = x2 – 3xy.
a) B – C = (2x2 – y2) – (x2 – 3xy)
= 2x2 – y2 – x2 + 3xy = (2x2 – x2) + 3xy – y2
= x2 + 3xy – y2;
b) (B – C) + A = (x2 + 3xy – y2) + (x2 – 2xy + y2)
= x2 + 3xy – y2 + x2 – 2xy + y2
= (x2 + x2) + (3xy – 2xy) + (y2 – y2)
= 2x2 + xy.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 11 Toán 8 Tập 1:
Khởi động trang 11 Toán 8 Tập 1: Ở lớp 7, ta đã học cách thực hiện phép cộng, phép trừ, phép nhân, phép chia các đa thức một biến.
Các phép tính với đa thức (nhiều biến) được thực hiện như thế nào?
Hoạt động 1 trang 11 Toán 8 Tập 1
Hoạt động 1 trang 11 Toán 8 Tập 1: Cho hai đa thức: P = x2 + 2xy + y2 và Q = x2 – 2xy + y2.
a) Viết tổng P + Q theo hàng ngang.
b) Nhóm các đơn thức đồng dạng với nhau.
c) Tính tổng P + Q bằng cách thực hiện phép tính trong từng nhóm.
Luyện tập 1 trang 11 Toán 8 Tập 1
Luyện tập 1 trang 11 Toán 8 Tập 1: Tính tổng của hai đa thức: M = x3 + y3 và N = x3 – y3.
Hoạt động 2 trang 12 Toán 8 Tập 1
Hoạt động 2 trang 12 Toán 8 Tập 1: Cho hai đa thức: P = x2 + 2xy + y2 và Q = x2 – 2xy + y2.
a) Viết hiệu P – Q theo hàng ngang, trong đó đa thức Q được đặt trong dấu ngoặc.
b) Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức Q, nhóm các đơn thức đổng dạng với nhau.
c) Tính tổng P – Q bằng cách thực hiện phép tính trong từng nhóm.
Hoạt động 3 trang 13 Toán 8 Tập 1
Hoạt động 3 trang 13 Toán 8 Tập 1:
a) Tính tích: 3x2 . 8x4;
b) Nêu quy tắc nhân hai đơn thức một biến.
Luyện tập 3 trang 13 Toán 8 Tập 1
Luyện tập 3 trang 13 Toán 8 Tập 1: Tính tích của hai đơn thức: x3y7 và −2x5y3.
Hoạt động 4 trang 13 Toán 8 Tập 1
Hoạt động 4 trang 13 Toán 8 Tập 1:
a) Tính tích: 11x3 . (x2 – x + 1);
b) Nêu quy tắc nhân đơn thức với đa thức trong trường hợp một biến.
Luyện tập 4 trang 14 Toán 8 Tập 1
Luyện tập 4 trang 14 Toán 8 Tập 1: Tính tích: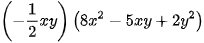 
Hoạt động 5 trang 14 Toán 8 Tập 1
Hoạt động 5 trang 14 Toán 8 Tập 1:
a) Tính tích: (x + 1)(x2 – x + 1);
b) Nêu quy tắc nhân hai đơn thức trong trường hợp một biến.
Luyện tập 5 trang 14 Toán 8 Tập 1
Luyện tập 5 trang 14 Toán 8 Tập 1: Tính: (x – y)(x – y).
Hoạt động 6 trang 15 Toán 8 Tập 1:
Hoạt động 6 trang 15 Toán 8 Tập 1: Tính tích: 9x5y4 . 2x4y2.
Luyện tập 6 trang 15 Toán 8 Tập 1
Luyện tập 6 trang 15 Toán 8 Tập 1: Cho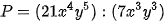 
. Tính giá trị của biểu thức P tại x = −0,5; y = −2.
Hoạt động 7 trang 16 Toán 8 Tập 1
Hoạt động 7 trang 16 Toán 8 Tập 1: Tính tích: (3xy)(x + y).
Luyện tập 7 trang 16 Toán 8 Tập 1
Luyện tập 7 trang 16 Toán 8 Tập 1: Tìm thương trong phép chia đa thức 12x3y3 – 6x4y3 + 21x3y4 cho đơn thức 3x3y3.
Bài 1 trang 16 Toán 8 Tập 1
Bài 1 trang 16 Toán 8 Tập 1: Thực hiện phép tính:
a) 
;
b) 
;
c)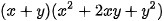 
;
d) 
.
Bài 2 trang 16 Toán 8 Tập 1
Bài 2 trang 16 Toán 8 Tập 1: Thực hiện phép tính:
a) 
b) 
Bài 3 trang 17 Toán 8 Tập 1
Bài 3 trang 17 Toán 8 Tập 1: Rút gọn biểu thức:
a) 
;
b) 
;
c) 
;
d) 
.
Bài 7 trang 17 Toán 8 Tập 1
Bài 7 trang 17 Toán 8 Tập 1: Khu vực của nhà bác Xuân có dạng hình vuông. Bác Xuân muốn dành một mảnh đất có dạng hình chữ nhật ở góc khu vườn để trồng rau (Hình 4). Biết diện tích của mảnh đất không trồng rau bằng 475 m2. Tính độ dài x (m) của khu vườn đó.
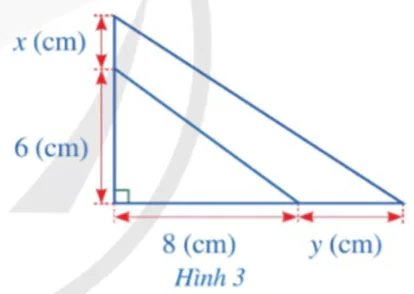
Bài 6 trang 17 Toán 8 Tập 1
Bài 6 trang 17 Toán 8 Tập 1: Bạn Hạnh dự định cắt một miếng bìa có dạng tam giác vuông với độ dài hai cạnh góc vuông lần lượt là 6 (cm), 8 (cm). Sau khi xem xét lại, bạn Hạnh quyết định tăng độ dài cạnh góc vuông 6 (cm) thêm x (cm) và tăng độ dài cạnh góc vuông 8 (cm) thêm y (cm) (Hình 3). Viết đa thức biểu thị diện tích phần tăng thêm của miếng bìa theo x và y.
Bài 5 trang 17 Toán 8 Tập 1
Bài 5 trang 17 Toán 8 Tập 1:
a) Chứng minh rằng biểu thức P = 5x(2 – x) – (x + 1)(x + 9) luôn nhận giá trị âm với mọi giá trị của biến x.
b) Chứng minh rằng biểu thức Q = 3x2 + x(x – 4y) – 2x(6 – 2y) + 12x + 1 luôn nhận giá trị dương với mọi giá trị của biến x và y.