Giải bài tập Hoạt động 7 trang 67 Toán 11 Tập 2 | Toán 11 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động 7 trang 67 Toán 11 Tập 2. Bài 2: Các quy tắc tính đạo hàm. Toán 11 - Cánh diều
Đề bài:
Bằng cách sử dụng kết quả = 1 tính đạo hàm của hàm số y = ex tại điểm x bất kì bằng định nghĩa.
Đáp án và cách giải chi tiết:
Xét ∆x là số gia của biến số tại điểm x bất kì.
Ta có: ∆y = f(x + ∆x) – f(x) = ex + ∆x – ex.
Suy ra = ex.1 = ex.
Vậy đạo hàm của hàm số y = ex tại điểm x bất kì là y' = ex.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 8 trang 72 Toán 11 Tập 2
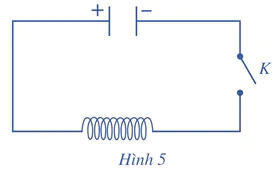
Cho mạch điện như Hình 5. Lúc đầu tụ điện có điện tích Q0. Khi đóng khóa K, tụ điện phóng điện qua cuộn dây; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức q(t) = Q0sinωt, trong đó ω là tốc độ góc. Biết rằng cường độ I(t) của dòng điện tại thời điểm t được tính theo công thức I(t) = q'(t). Cho biết Q0 = 10–8 (C) và ω = 106π (rad/s). Tính cường độ dòng điện tại thời điểm t = 6 (s) (tính chính xác đến 10–5 mA)
Bài 7 trang 72 Toán 11 Tập 2
Một viên đạn được bắn từ mặt đất theo phương thẳng đứng với tốc độ ban đầu v0 = 196 m/s (bỏ qua sức cản của không khí). Tìm thời điểm mà tốc độ của viên đạn bằng 0. Khi đó viên đạn cách mặt đất bao nhiêu mét (lấy g = 9,8 m/s2)?
Bài 6 trang 72 Toán 11 Tập 2
Viết phương trình tiếp tuyến của đồ thị mỗi hàm số sau:
a) y = x3 – 3x2 + 4 tại điểm có hoành độ x0 = 2;
b) y = lnx tại điểm có hoành độ x0 = e;
c) y = ex tại điểm có hoành độ x0 = 0.
Bài 5 trang 72 Toán 11 Tập 2
Tìm đạo hàm của mỗi hàm số sau:
a) y = sin3x + sin2x
b) y = log2(2x + 1) + 3−2x + 1
Bài 4 trang 71 Toán 11 Tập 2
Cho hàm số f(x) = 23x + 2.
a) Hàm số f(x) là hàm hợp của các hàm số nào?
b) Tìm đạo hàm của f(x)
Bài 2 trang 71 Toán 11 Tập 2
Cho u = u(x), v = v(x), w = w(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định.
Chứng minh rằng (u . v . w)' = u' . v . w + u . v' . w + u . v . w'.
Bài 1 trang 71 Toán 11 Tập 2
Cho u = u(x), v = v(x), w = w(x) là các hàm số tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng?
a) (u + v + w)' = u' + v' + w';
b) (u + v – w)' = u' + v' – w';
c) (uv)' = u'v';
d) với v = v(x) ≠ 0, v' = v'(x) ≠ 0.
Câu hỏi khởi động trang 64 Toán 11 Tập 2
Ta có thể tính đạo hàm của hàm số bằng cách sử dụng định nghĩa. Tuy nhiên, cách làm đó là không thuận lợi khi hàm số được cho bằng những công thức phức tạp. Trong thực tiễn, để tính đạo hàm của một hàm số ta thường sử dụng các quy tắc tính đạo hàm để đưa việc tính toán đó về tính đạo hàm của những hàm số sơ cấp cơ bản.
Đạo hàm của những hàm số sơ cấp cơ bản là gì?
Làm thế nào để thực hiện được các quy tắc đạo hàm?
Hoạt động 1 trang 64 Toán 11 Tập 2
a) Tính đạo hàm của hàm số y = x2 tại điểm x0 bất kì bằng định nghĩa.
b) Dự đoán đạo hàm của hàm số y = xn tại điểm x bất kì
Luyện tập 1 trang 64 Toán 11 Tập 2
Cho hàm số y = x22
a) Tính đạo hàm của hàm số trên tại điểm x bất kì.
b) Tính đạo hàm của hàm số trên tại điểm x0 = 1.
Hoạt động 3 trang 65 Toán 11 Tập 2
Bằng cách sử dụng kết quả = 1 tính đạo hàm của hàm số y = sinx tại điểm x bất kì bằng định nghĩa.
Luyện tập 3 trang 65 Toán 11 Tập 2
Tính đạo hàm của hàm số f(x) = sinx tại điểm x0 = .
Hoạt động 4 trang 65 Toán 11 Tập 2
Bằng định nghĩa, tính đạo hàm của hàm số y = cosx tại điểm x bất kì.
Luyện tập 4 trang 66 Toán 11 Tập 2
Một vật dao động theo phương trình f(x) = cosx, trong đó x là thời gian tính theo giây. Tính vận tốc tức thời của vật tại thời điểm x0 = 2.
Hoạt động 5 trang 66 Toán 11 Tập 2
Bằng định nghĩa, tính đạo hàm của hàm số y = tanx tại điểm x bất kì, x ≠ + kπ (k ∈ ℤ).
Hoạt động 6 trang 66 Toán 11 Tập 2
Bằng định nghĩa, tính đạo hàm của hàm số y = cotx tại điểm x bất kì, x ≠ kπ (k ∈ ℤ).
Luyện tập 7 trang 67 Toán 11 Tập 2
Tính đạo hàm của hàm số f(x) = 10x tại điểm x0 = –1.
Hoạt động 8 trang 67 Toán 11 Tập 2
Bằng cách sử dụng kết quả = 1 tính đạo hàm của hàm số y = lnx tại điểm x dương bất kì bằng định nghĩa.
Luyện tập 8 trang 67 Toán 11 Tập 2
Tính đạo hàm của hàm số f(x) = logx tại điểm x0 = .
Hoạt động 9 trang 68 Toán 11 Tập 2
Cho hai hàm số f(x), g(x) xác định trên khoảng (a; b) cùng có đạo hàm tại điểm x0 ∈ (a; b).
a) Xét hàm số h(x) = f(x) + g(x), x ∈ (a; b). So sánh:
và
b) Nêu nhận xét về h'(x0) và f'(x0) + g’(x0).