Giải bài tập Bài 6.36 trang 26 Toán 11 Tập 2 | Toán 11 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 6.36 trang 26 Toán 11 Tập 2. Bài tập cuối chương 6. Toán 11 - Kết nối tri thức
Đề bài:
Giải các phương trình sau:
a) 31 – 2x = 4x;
b) log3(x + 1) + log3(x + 4) = 2.
Đáp án và cách giải chi tiết:
a) 31 – 2x = 4x
Lấy lôgarit cơ số 3 hai vế của phương trình ta được
log3 31 – 2x = log3 4x
⇔ 1 – 2x = x log34
⇔ (2 + log34)x = 1
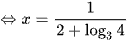
Vậy phương trình đã cho có nghiệm duy nhất là 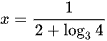 .
.
b) log3(x + 1) + log3(x + 4) = 2
Ta có log3(x + 1) + log3(x + 4) = 2
⇔ log3[(x + 1)(x + 4)] = 2
⇔ (x + 1)(x + 4) = 32
⇔ x2 + 5x + 4 = 9
⇔ x2 + 5x – 5 = 0
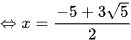 hoặc
hoặc 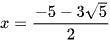
Loại nghiệm 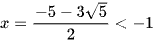
Vậy phương trình đã cho có nghiệm duy nhất là 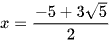 .
.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 6.27 trang 25 Toán 11 Tập 2
Cho hai số thực dương x, y và hai số thực α, β tùy ý. Khẳng định nào sau đây là sai?
A. xα ∙ xβ = xα + β.
B. xα ∙ yβ = (xy)α + β.
C. (xα)β = xα ∙ β.
D. (xy)α = xα ∙ yα.
Bài 6.29 trang 25 Toán 11 Tập 2
Cho hai số thực dương a, b với a ≠ 1. Khẳng định nào sau đây là đúng?
A. loga(a3b2) = 3 + logab.
B. loga(a3b2) = 3 + 2logab.
C. loga(a3b2) =  logab.
logab.
D. loga(a3b2) =  .
.
Bài 6.30 trang 25 Toán 11 Tập 2
Cho bốn số thực dương a, b, x, y với a, b ≠ 1. Khẳng định nào sau đây là sai?
A. loga(xy) = logax + logay.
B. .
C. .
D. logab ∙ logbx = logax.
Bài 6.31 trang 25 Toán 11 Tập 2
Đặt log25 = a, log35 = b. Khi đó, log65 tính theo a và b bằng
A. .
B. .
C. a2 + b2.
D. a + b.
Bài 6.32 trang 25 Toán 11 Tập 2
Cho hàm số y = 2x. Khẳng định nào sau đây là sai?
A. Tập xác định của hàm số là ℝ.
B. Tập giá trị của hàm số là (0; + ∞).
C. Đồ thị của hàm số cắt trục Ox tại đúng một điểm.
D. Hàm số đồng biến trên tập xác định của nó.
Bài 6.33 trang 25 Toán 11 Tập 2
Hàm số nào sau đây đồng biến trên tập xác định của nó?
A. y = log0,5x.
B. y = e– x.
C. .
D. y = ln x.
Bài 6.34 trang 25 Toán 11 Tập 2
Cho đồ thị ba hàm số y = logax, y = logbx và y = logcx như hình bên. Mệnh đề nào sau đây là đúng?

A. a > b > c.
B. b > a > c.
C. a > c > b.
D. b > c > a.
Bài 6.39 trang 26 Toán 11 Tập 2
Giả sử quá trình nuôi cấy vi khuẩn tuân theo quy luật tăng trưởng tự do. Khi đó, nếu gọi N0 là số lượng vi khuẩn ban đầu và N(t) là số lượng vi khuẩn sau t giờ thì ta có:
, trong đó r là tỉ lệ tăng trưởng vi khuẩn mỗi giờ. Giả sử ban đầu có 500 con vi khuẩn và sau 1 giờ tăng lên 800 con. Hỏi:
a) Sau 5 giờ thì số lượng vi khuẩn là khoảng bao nhiêu con?
b) Sau bao lâu thì số lượng vi khuẩn ban đầu sẽ tăng lên gấp đôi?
Bài 6.40 trang 26 Toán 11 Tập 2
Vào năm 1938, nhà vật lí Frank Benford đã đưa ra một phương pháp để xác định xem một bộ số đã được chọn ngẫu nhiên hay đã được chọn theo cách thủ công. Nếu bộ số này không được chọn ngẫu nhiên thì công thức Benford sau sẽ được dùng ước tính xác suất P để chữ số d là chữ số đầu tiên của bộ số đó: . (Theo F.Benford, The Law of Anomalous Numbers, Proc. Am. Philos. Soc. 78 (1938), 551 – 572).
Chẳng hạn, xác suất để chữ số đầu tiên là 9 bằng khoảng 4,6% (thay d = 9 trong công thức Benford để tính P).
a) Viết công thức tìm chữ số d nếu cho trước xác suất P.
b) Tìm chữ số có xác suất bằng 9,7% được chọn.
c) Tính xác suất để chữ số đầu tiên là 1.
Bài 6.37 trang 26 Toán 11 Tập 2
Tìm tập xác định của các hàm số sau:
a)  ;
;
b) y = ln(1 – lnx).
Bài 6.38 trang 26 Toán 11 Tập 2
Lạm phát là sự tăng mức giá chung một cách liên tục của hàng hoá và dịch vụ theo thời gian, tức là sự mất giá trị của một loại tiền tệ nào đó. Chẳng hạn, nếu lạm phát là 5% một năm thì sức mua của 1 triệu đồng sau một năm chỉ còn là 950 nghìn đồng (vì đã giảm mất 5% của 1 triệu đồng, tức là 50 000 đồng). Nói chung, nếu tỉ lệ lạm phát trung bình là r% một năm thì tổng số tiền P ban đầu, sau n năm số tiền đó chỉ còn giá trị là 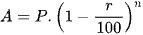 .
.
a) Nếu tỉ lệ lạm phát là 8% một năm thì sức mua của 100 triệu đồng sau hai năm sẽ còn lại bao nhiêu?
b) Nếu sức mua của 100 triệu đồng sau hai năm chỉ còn là 90 triệu đồng thì tỉ lệ lạm phát trung bình của hai năm đó là bao nhiêu?
c) Nếu tỉ lệ lạm phát là 5% một năm thì sau bao nhiêu năm sức mua của số tiền ban đầu chỉ còn lại một nửa?

 ta được
ta được