Giải bài tập Bài 4.36 trang 102 Toán 11 Tập 1 | Toán 11 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 4.36 trang 102 Toán 11 Tập 1. Bài tập cuối chương 4. Toán 11 - Kết nối tri thức
Đề bài:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Đường thẳng SB song song với mặt phẳng
A. (CDM).
B. (ACM).
C. (ADM).
D. (ACD).
Đáp án và cách giải chi tiết:
Đáp án đúng là: B
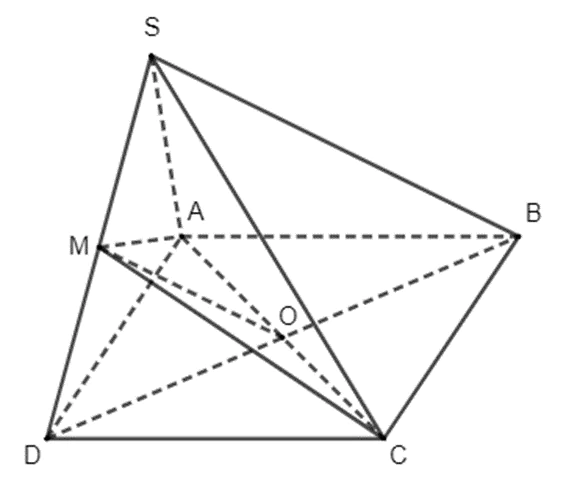
Gọi O là tâm của hình bình hành ABCD, khi đó hai đường chéo AC và BD của hình bình hành ABCD cắt nhau tại trung điểm O của mỗi đường.
Xét tam giác SBD có M, O lần lượt là trung điểm của SD và BD nên MO là đường trung bình của tam giác SBD, suy ra MO // SB.
Vì O thuộc AC nên O thuộc mặt phẳng (ACM) và M thuộc mặt phẳng (ACM) nên mặt phẳng (ACM) chứa đường thẳng OM.
Khi đó ta có đường thẳng SB song song với đường thẳng OM và đường thẳng OM nằm trong mặt phẳng (ACM), do vậy đường thẳng SB song song với mặt phẳng (ACM).
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 4.35 trang 102 Toán 11 Tập 1
Cho đường thẳng a song song với mặt phẳng (P). Mặt phẳng (Q) chứa đường thẳng a và cắt mặt phẳng (P) theo giao tuyến là đường thẳng b. Vị trí tương đối của hai đường thẳng a và b là
A. chéo nhau.
B. cắt nhau.
C. song song.
D. trùng nhau.
Bài 4.37 trang 102 Toán 11 Tập 1
Cho hình hộp ABCD.A'B'C'D'. Mặt phẳng (AB'D') song song với mặt phẳng
A. (ABCD).
B. (BCC'B').
C. (BDA').
D. (BDC').
Bài 4.38 trang 102 Toán 11 Tập 1
Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng a cắt các mặt phẳng (P), (Q), (R) lần lượt tại A, B, C sao cho và đường thẳng b cắt các mặt phẳng (P), (Q), (R) lần lượt tại A', B', C'. Tỉ số bằng
A.
B.
C.
D.
Bài 4.39 trang 102 Toán 11 Tập 1
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số
A.
B.
C.
D.
Bài 4.40 trang 102 Toán 11 Tập 1
Cho hình hộp ABCD.A'B'C'D'. Gọi M, M' lần lượt là trung điểm của các cạnh BC, B'C'. Hình chiếu của ∆B'DM qua phép chiếu song song trên (A'B'C'D') theo phương chiếu AA' là
A. ∆B'A'M'.
B. ∆C'D'M'.
C. ∆DMM'.
D. ∆B'D'M'.
Bài 4.41 trang 103 Toán 11 Tập 1
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD và AB < CD. Xác định giao tuyến của hai mặt phẳng sau:
a) (SAD) và (SBC);
b) (SAB) và (SCD);
c) (SAC) và (SBD).
Bài 4.42 trang 103 Toán 11 Tập 1
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, AA'.
a) Xác định giao điểm của mặt phẳng (MNP) với đường thẳng B'C.
b) Gọi K là giao điểm của mặt phẳng (MNP) với đường thẳng B'C. Tính tỉ số .
Bài 4.43 trang 103 Toán 11 Tập 1
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trên cạnh SC và cạnh AB lần lượt lấy điểm M và N sao cho CM = 2SM và BN = 2AN.
a) Xác định giao điểm K của mặt phẳng (ABM) với đường thẳng SD. Tính tỉ số .
b) Chứng minh rằng MN // (SAD).
Bài 4.44 trang 103 Toán 11 Tập 1
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G, K lần lượt là trọng tâm của các tam giác SAD, SCD.
a) Chứng minh rằng GK // (ABCD).
b) Mặt phẳng chứa đường thẳng GK và song song với mặt phẳng (ABCD) cắt các cạnh SA, SB, SC, SD lần lượt tại M, N, E, F. Chứng minh rằng tứ giác MNEF là hình bình hành.
Bài 4.45 trang 103 Toán 11 Tập 1
Cho hình hộp ABCD.A'B'C'D'. Gọi M, N lần lượt là trung điểm của cạnh AD, A'B'. Chứng minh rằng:
a) BD // B'D', (A'BD) // (CB'D') và MN // (BDD'B');
b) Đường thẳng AC' đi qua trọng tâm G của tam giác A'BD.
Bài 4.46 trang 103 Toán 11 Tập 1
Cho tứ diện ABCD. Trên cạnh AB lấy điểm M sao cho BM = 3AM. Mặt phẳng (P) đi qua M song song với hai đường thẳng AD và BC.
a) Xác định giao điểm K của mặt phẳng (P) với đường thẳng CD.
b) Tính tỉ số