Giải bài tập Bài 2.11 trang 59 Toán 12 Tập 1 | SGK Toán 12 - Kết nối tri thức

Bài 2.1 trang 58 Toán 12 Tập 1: Trong không gian, cho ba vectơ $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{c}}$ phân biệt và đều khác $\overrightarrow{0}$. Những mệnh đề nào sau đây là đúng?

a) Nếu $\overrightarrow{\mathrm{a}} \mathrm{và} \overrightarrow{\mathrm{b}}$ đều cùng hướng với $\overrightarrow{\mathrm{c}}$ thì $\overrightarrow{\mathrm{a}} \mathrm{và} \overrightarrow{\mathrm{b}}$ cùng hướng.

b) Nếu $\overrightarrow{\mathrm{a}} \mathrm{và} \overrightarrow{\mathrm{b}}$ đều ngược hướng với $\overrightarrow{\mathrm{c}}$ thì $\overrightarrow{\mathrm{a}} \mathrm{và} \overrightarrow{\mathrm{b}}$ cùng hướng.

c) Nếu $\overrightarrow{\mathrm{a}} \mathrm{và} \overrightarrow{\mathrm{b}}$ đều cùng hướng với $\overrightarrow{\mathrm{c}}$ thì $\overrightarrow{\mathrm{a}} \mathrm{và} \overrightarrow{\mathrm{b}}$ ngược hướng.

d) Nếu $\overrightarrow{\mathrm{a}} \mathrm{và} \overrightarrow{\mathrm{b}}$ đều ngược hướng với $\overrightarrow{\mathrm{c}}$ thì $\overrightarrow{\mathrm{a}} \mathrm{và} \overrightarrow{\mathrm{b}}$ ngược hướng.

Bài 2.2 trang 58 Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2, AD = 3 và AA' = 4. Tính độ dài của các vectơ  $\overrightarrow{\mathrm{BB}\text{'}}, \overrightarrow{\mathrm{BD}} \mathrm{và} \overrightarrow{\mathrm{BD}\text{'}}$.

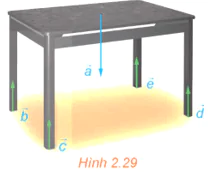
Bài 2.3 trang 58 Toán 12 Tập 1: Một chiếc bàn cân đối hình chữ nhật được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn và bốn chân bàn vuông góc với mặt sàn như Hình 2.29. Trọng lực tác dụng lên bàn (biểu thị bởi vectơ $\overrightarrow{\mathrm{a}}$) phân tán đều qua bốn chân bàn và gây nên các phản lực từ mặt sàn lên các chân bàn (biểu thị bởi các vectơ $\overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{c}}, \overrightarrow{\mathrm{d}}, \overrightarrow{\mathrm{e}}$).

a) Hãy chỉ ra mối quan hệ về phương và hướng của các vectơ $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{c}}, \overrightarrow{\mathrm{d}} \mathrm{và} \overrightarrow{\mathrm{e}}$

b) Giải thích vì sao các vectơ $\overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{c}}, \overrightarrow{\mathrm{d}}, \overrightarrow{\mathrm{e}}$ đôi một bằng nhau.

Bài 2.4 trang 58 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng:

a) $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{DD}\text{'}}+\overrightarrow{\mathrm{C}\text{'}\mathrm{D}\text{'}}=\overrightarrow{\mathrm{CC}\text{'}}$;

b) $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{CD}\text{'}}-\overrightarrow{\mathrm{CC}\text{'}}=\overrightarrow{0}$;

c) $\overrightarrow{\mathrm{BC}}-\overrightarrow{\mathrm{CC}\text{'}}+\overrightarrow{\mathrm{DC}}=\overrightarrow{\mathrm{A}\text{'}\mathrm{C}}$;

Bài 2.5 trang 58 Toán 12 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C' có $\overrightarrow{\mathrm{AA}\text{'}}=\overrightarrow{\mathrm{a}}; \overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{b}} \mathrm{và} \overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{c}}$. Hãy biểu diễn các vectơ sau qua các vectơ $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{c}}$

a) $\overrightarrow{\mathrm{AB}\text{'}}$;

b)  $\overrightarrow{\mathrm{B}\text{'}\mathrm{C}}$;

c) $\overrightarrow{\mathrm{BC}\text{'}}$.

Bài 2.6 trang 58 Toán 12 Tập 1: Cho hình chóp tứ giác S.ABCD. Chứng minh rằng tứ giác ABCD là hình bình hành nếu và chỉ nếu $\overrightarrow{\mathrm{SA}}+\overrightarrow{\mathrm{SC}}=\overrightarrow{\mathrm{SB}}+\overrightarrow{\mathrm{SD}}$

Bài 2.7 trang 58 Toán 12 Tập 1: Cho hình chóp S.ABC. Trên cạnh SA, lấy điểm M sao cho SM = 2AM. Trên cạnh BC, lấy điểm N sao cho CN = 2BN. Chứng minh rằng $\overrightarrow{\mathrm{MN}}=\frac{1}{3}\left(\overrightarrow{\mathrm{SA}}+\overrightarrow{\mathrm{BC}}\right)+\overrightarrow{\mathrm{AB}}$

Bài 2.8 trang 58 Toán 12 Tập 1: Trong Luyện tập 8, ta đã biết trọng tâm của tứ diện ABCD là một điểm I thỏa mãn $\overrightarrow{\mathrm{AI}}=3\overrightarrow{\mathrm{IG}}$, ở đó G là trọng tâm của tam giác BCD. Áp dụng tính chất trên để tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối rubik là 8 cm (H.2.30).

Bài 2.9 trang 59 Toán 12 Tập 1: Ba sợi dây không giãn với khối lượng không đáng kể được buộc chung một đầu và được kéo căng về ba hướng khác nhau (H.2.31). Nếu các lực kéo làm cho ba sợi dây ở trạng thái đứng yên thì khi đó ba sợi dây nằm trên cùng một mặt phẳng. Hãy giải thích vì sao.

Bài 2.10 trang 59 Toán 12 Tập 1: Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có độ dài mỗi cạnh đáy bằng 1 và độ dài mỗi cạnh bên bằng 2. Hãy tính góc giữa các cặp vectơ sau đây và tính tích vô hướng của mỗi cặp vectơ đó:

a) $\overrightarrow{\mathrm{AA}\text{'}} \mathrm{và} \overrightarrow{\mathrm{C}\text{'}\mathrm{C}}$

b) $\overrightarrow{\mathrm{AA}\text{'}} \mathrm{và} \overrightarrow{\mathrm{BC}}$

c) $\overrightarrow{\mathrm{AC}} \mathrm{và} \overrightarrow{\mathrm{B}\text{'}\mathrm{A}\text{'}}$

Bài 2.12 trang 59 Toán 12 Tập 1: Cho tứ diện ABCD. Chứng minh rằng

a) $\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{CD}}=\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{BC}}.\overrightarrow{\mathrm{DC}}$

b) $\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{DB}}+\overrightarrow{\mathrm{AD}}.\overrightarrow{\mathrm{BC}}=0$

Ở lớp 10, ta đã biết về vectơ trong mặt phẳng và biết sử dụng vectơ để biểu thị các đại lượng có hướng và độ lớn trong mặt phẳng, ví dụ như vận tốc hay lực. Đối với các đại lượng có hướng trong không gian, ta có thể sử dụng vectơ để biểu diễn chúng hay không? Các phép toán vectơ trong trường hợp này giống và khác như thế nào với các phép toán vectơ trong mặt phẳng?

Trong Hình 2.2, lực căng dây (được tạo ra bởi sức nặng của kiện hàng) được thể hiện bởi các đoạn thẳng có mũi tên màu đỏ.

a) Các đoạn thẳng này cho biết gì về hướng và độ lớn của các lực căng dây?

b) Các đoạn thẳng này có cùng nằm trong một mặt phẳng không?

Hình 2.3 cho ta ví dụ về một số đại lượng có thể được biểu diễn bởi vectơ trong không gian. Hãy tìm thêm một số ví dụ tương tự.

Cho hình lập phương ABCD.A'B'C'D' (H.2.6). Trong các vectơ ,, :

a) Hai vectơ nào có giá cùng nằm trong mặt phẳng (ABCD)?

b) Hai vectơ nào có cùng độ dài?

Cho hình hộp ABCD.A'B'C'D' (H.2.7).

a) So sánh độ dài của hai vectơ và .

b) Nhận xét về giá của hai vectơ và .

c) Hai vectơ và có cùng phương không? Có cùng hướng không?

Nếu hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó có bằng nhau không?

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.

a) Trong ba vectơ , và vectơ nào bằng vectơ ?

b) Gọi M là một điểm thuộc cạnh AD. Xác định điểm sao cho .

Một tòa nhà có chiều cao của các tầng là như nhau. Một chiếc thang máy di chuyển từ tầng 15 lên tầng 22 của tòa nhà, sau đó di chuyển từ tầng 22 lần tầng 29. Các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển có bằng nhau không? Giải thích vì sao.

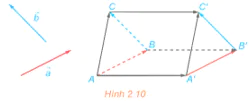
Trong không gian, cho hai vectơ và 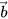không cùng phương. Lấy điểm A và vẽ các vectơ , . Lấy điểm A' khác A và vẽ các vectơ , 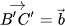(H.2.10).

a) Giải thích vì sao và .

b) Giải thích vì sao AA'C'C là hình bình hành, từ đó suy ra 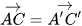.