Giải bài tập Bài 2 trang 63 Toán 11 Tập 2 | Toán 11 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 2 trang 63 Toán 11 Tập 2. Bài 1: Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm. Toán 11 - Cánh diều
Đề bài:
Chứng minh rằng hàm số f(x) = |x| không có đạo hàm tại điểm x0 = 0, nhưng có đạo hàm tại mọi điểm x ≠ 0
Đáp án và cách giải chi tiết:
Xét ∆x là số gia của biến số tại điểm x0 = 0.
Ta có ∆y = f(0 + ∆x) – f(0) = |∆x| – |0| = |∆x|.
Suy ra 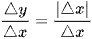
Ta thấy ![]()
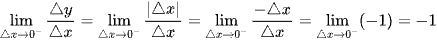
Do đó 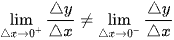 nên không tồn tại
nên không tồn tại 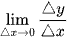 .
.
Vậy hàm số f(x) = |x| không có đạo hàm tại điểm x0 = 0.
Ta có hàm số 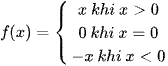
⦁ Với x > 0 ta có hàm số f(x) = x.
Xét ∆x là số gia của biến số tại điểm x > 0.
Ta có ∆y = f(x + ∆x) – f(x) = (x + ∆x) – x = ∆x.
Suy ra 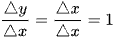
Ta thấy 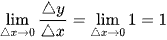
Do đó với x > 0 thì hàm số có đạo hàm f’(x) = 1.
⦁ Với x < 0 ta có hàm số f(x) = –x.
Xét ∆x là số gia của biến số tại điểm x < 0.
Ta có ∆y = f(x + ∆x) – f(x) = – (x + ∆x) + x = –∆x.
Suy ra 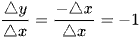
Ta thấy 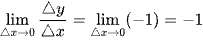
Do đó với x < 0 thì hàm số có đạo hàm f’(x) = –1.
Vậy hàm số f(x) = |x| không có đạo hàm tại x0 = 0, nhưng có đạo hàm tại mọi điểm x ≠ 0.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 63 Toán 11 Tập 2
Tính đạo hàm của hàm số f(x) = 3x3 – 1 tại điểm x0 = 1 bằng định nghĩa:
Bài 3 trang 63 Toán 11 Tập 2
Cho hàm y = –2x2 + x có đồ thị (C).
a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2.
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; – 6)
Bài 4 trang 63 Toán 11 Tập 2
Giả sử chi phí C (USD) để sản xuất Q máy vô tuyến là C(Q) = Q2 + 80Q + 3500.
a) Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ Q sản phẩm lên Q + 1 sản phẩm. Giả sử chi phí biên được xác định bởi hàm số C’(Q). Tìm hàm chi phí biên.
b) Tìm C’(90) và giải thích ý nghĩa kết quả tìm được.
Câu hỏi khởi động trang 59 Toán 11 Tập 2
Tên lửa vũ trụ là phương tiện được chế tạo đặc biệt giúp con người thực hiện các sứ mệnh trong không gian như: tiếp cận đến các hành tinh ngoài Trái Đất, vận chuyển con người và thiết bị lên vũ trụ, ... (Hình 1).

Nếu quỹ đạo chuyển động của tên lửa được miêu tả bằng hàm số theo thời gian thì đại lượng nào biểu thị độ nhanh chậm của chuyển động tại một thời điểm?
Hoạt động 1 trang 60 Toán 11 Tập 2
Tính vận tốc tức thời của viên bi tại thời điểm x0 = 1 (s) trong bài toán tìm vận tốc tức thời nêu ở trên.
Luyện tập 1 trang 61 Toán 11 Tập 2
Tính đạo hàm của hàm số f(x) = tại x0 = 2 bằng định nghĩa.
Luyện tập 2 trang 62 Toán 11 Tập 2
Tính đạo hàm của hàm số f(x) = x3 tại điểm x bất kì bằng định nghĩa.
Luyện tập 3 trang 63 Toán 11 Tập 2
Viết phương trình tiếp tuyến của đồ thị hàm số y = tại điểm N(1; 1).
Hoạt động 2 trang 62 Toán 11 Tập 2
Cho hàm số y = f(x) có đồ thị (C), một điểm M0 cố định thuộc (C) có hoành độ x0. Với mỗi điểm M thuộc (C) khác M0, kí hiệu xM là hoành độ của điểm M và kM là hệ số góc của cát tuyến M0M. Giả sử tồn tại giới hạn hữu hạn  . Khi đó, ta coi đường thẳng M0T đi qua M0 và có hệ số góc k0 là vị trí giới hạn của cát tuyến M0M khi điểm M di chuyển dọc theo (C) dần tới M0.s
. Khi đó, ta coi đường thẳng M0T đi qua M0 và có hệ số góc k0 là vị trí giới hạn của cát tuyến M0M khi điểm M di chuyển dọc theo (C) dần tới M0.s
Đường thẳng M0T được gọi là tiếp tuyến của (C) tại điểm M0, còn M0 được gọi là tiếp điểm (Hình 3).
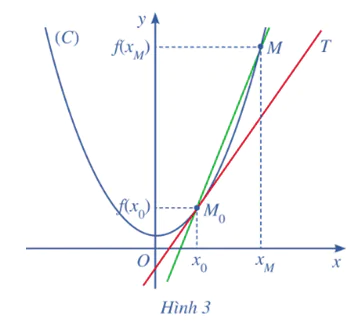
a) Xác định hệ số góc k0 của tiếp tuyến M0T theo x0.
b) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M0.