Giải bài tập Bài 1 trang 31 SBT Toán 12 Tập 1 | SBT Toán 12 - Chân trời sáng tạo (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 1 trang 31 SBT Toán 12 Tập 1. Bài 4. Khảo sát và vẽ đồ thị một số hàm số cơ bản. SBT Toán 12 - Chân trời sáng tạo (SBT)
Đề bài:
Khảo sát và vẽ đồ thị của các hàm số sau:
a) y = x(x2 – 4x);
b) y = −x3 + 3x2 – 2.
Đáp án và cách giải chi tiết:
a) y = x(x2 – 4x) = x3 – 4x2
Tập xác định: D = ℝ.
Ta có: y' = 3x2 – 8x
y' = 0 ⇔ x = 0 hoặc x = .
Ta có bảng biến thiên:
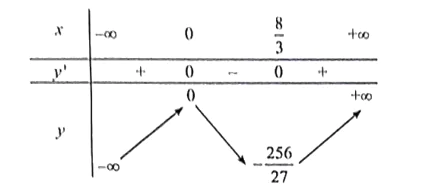
Hàm số đồng biến trên các khoảng (−∞; 0) và .
Hàm số nghịch biến trên khoảng .
Hàm số đạt cực đại tại x = 0, yCĐ = 0.
Hàm số đạt cực tiểu tại x = , yCT = .
Đồ thị hàm số:
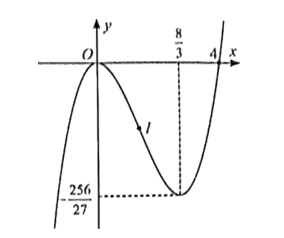
b) y = −x3 + 3x2 – 2
Tập xác định: D = ℝ.
Ta có: y' = −3x2 + 6x
y' = 0 ⇔ x = 0 hoặc x = 2.
Ta có bảng biến thiên:
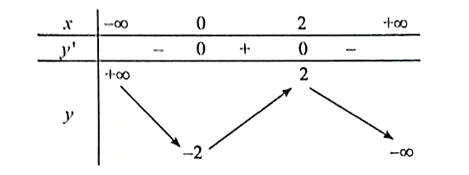
Hàm số đồng biến trên khoảng (0; 2).
Hàm số nghịch biến trên các khoảng (−∞; 0) và (2; +∞).
Hàm số đạt cực đại tại x = 2, yCĐ = 2.
Hàm số đạt cực tiểu tại x = 0, yCT = −2.
Đồ thị hàm số:
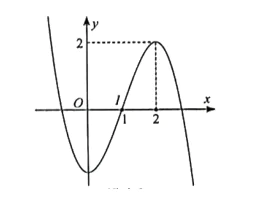
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 2 trang 31 SBT Toán 12 Tập 1
Cho hàm số y = (m – 1)x3 + 2(m + 1)x2 – x + m – 1 (m là tham số)
a) Khảo sát và vẽ đồ thị của hàm số khi m = −1.
b) Tìm giá trị của m để tâm đối xứng của đồ thị hàm số có hoành độ x0 = −2.
Bài 3 trang 31 SBT Toán 12 Tập 1
Cho hàm số y = 2x3 + 6x2 – x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại tâm đối xứng của nó.
Bài 4 trang 31 SBT Toán 12 Tập 1
Với giá trị nào của m thì đồ thị của hàm số y = −x3 – 3x2 + mx + 1 có tâm đối xứng nằm trên trục Ox? Khi đó, có thể kết luận gì về số giao điểm của đồ thị hàm số với trục hoành?
Bài 5 trang 31 SBT Toán 12 Tập 1
Khảo sát và vẽ đồ thị của các hàm số sau:
a) y = 3 + ;
b) y = 2 - .
Bài 6 trang 32 SBT Toán 12 Tập 1
Ta đã biết đồ thị hàm số y = có tiệm cận đứng là đường thẳng x = −1 và tiệm cận ngang là đường thẳng y = 2.
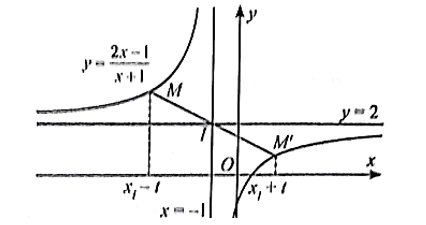
a) Tìm tọa độ giao điểm I của đường tiệm cận.
b) Với t tùy ý (t ≠ 0), gọi M và M' lần lượt là hai điểm trên đồ thị hàm số có hoành độ lần lượt là xM = xI – t và xM' = xI + t. Tìm các tung độ y(xM) và y(xM'). Từ đó, chứng minh rằng hai điểm M và M' đối xứng với nhau qua I.
Bài 7 trang 32 SBT Toán 12 Tập 1
Cho hàm số y = . Chứng tỏ rằng đường thẳng y = −x cắt đồ thị hàm số đã cho tại hai điểm phân biệt.
Bài 8 trang 32 SBT Toán 12 Tập 1
Khảo sát và vẽ đồ thị của các hàm số sau:
a) y = ;
b) y = -2x + .
Bài 9 trang 32 SBT Toán 12 Tập 1
Cho hàm số y = .
a) Tìm tọa độ giao điểm I của hai đường tiệm cận của đồ thị hàm số.
b) Với t tùy ý (t ≠ 0), gọi M và M' lần lượt là hai điểm trên đồ thị hàm số có hoành độ lần lượt là xM = xI – t và xM' = xI + t. so sánh các tung độ yM và yM'. Từ đó, suy ra rằng hai điểm M và M' đối xứng với nhau qua I.
Bài 10 trang 32 SBT Toán 12 Tập 1
Cho hàm số y = (m là tham số).
Tìm điều kiện của m để đồ thị hàm số đã cho có một nhánh nằm hoàn toàn trong góc phần tư thứ nhất của hệ trục Oxy.
Bài 11 trang 32 SBT Toán 12 Tập 1
Cho hàm số y = (m là tham số).
a) Tìm m để đồ thị hàm số đã cho có hai điểm cực trị.
b) Chứng tỏ rằng khi m = 2, hàm số có hai điểm cực trị. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số này.