Giải bài tập Bài 4 trang 17 SBT Toán 12 Tập 1 | SBT Toán 12 - Chân trời sáng tạo (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 4 trang 17 SBT Toán 12 Tập 1. Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số. SBT Toán 12 - Chân trời sáng tạo (SBT)
Đề bài:
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) y = trên khoảng (1; +∞);
b) y = trên nửa khoảng [0; +∞);
c) y = trên nửa khoảng ;
d) y = trên đoạn [−2; 4].
Đáp án và cách giải chi tiết:
a) y = trên khoảng (1; +∞).
Tập xác định: D = ℝ\.
Ta có: y' =
y' = 0 ⇔ = 0 ⇔ x = 2 hoặc x = −1 (loại do −1∉ (1; +∞)).
Ta có bảng biến thiên:
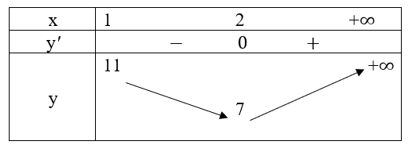
Do đó, = y(2) = 7, hàm số không có giá trị lớn nhất (1; +∞).
b) y = trên nửa khoảng [0; +∞).
Tập xác định: D = ℝ\.
Ta có: y' = > 0, với mọi x ∈ [0; +∞).
Ta có bản biến thiên:
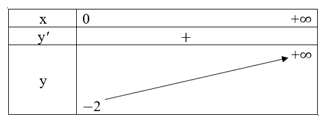
Do đó, = y(0) = −2, hàm số không có giá trị lớn nhất trên [0; +∞).
c) y = trên nửa khoảng .
Tập xác định: D = ℝ\.
Ta có: y' =
y' = 0 ⇔ = 0 ⇔ x = hoặc x = (loại do ).
Ta có bảng biến thiên:
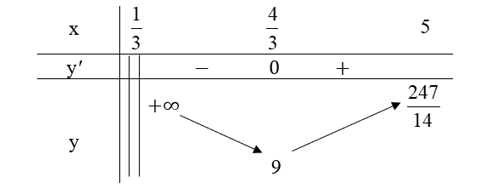
Do đó, = 9, hàm số không có giá trị lớn nhất trên .
d) y = trên đoạn [−2; 4].
Tập xác định: D = ℝ\.
Ta có: y' =
y' = 0 ⇔ = 0 ⇔ x = hoặc x = (loại do ∉ [−2; 4]).
Ta có bảng biến thiên:
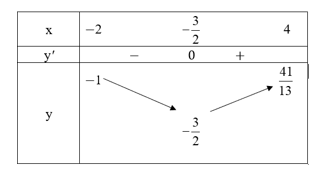
Do đó, .
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 16 SBT Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 2.

Bài 2 trang 17 SBT Toán 12 Tập 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) y = x3 – 8x2 – 12x + 1 trên đoạn [−2; 9];
b) y = −2x3 + 9x2 – 17 trên nửa khoảng (−∞; 4];
c) y = x3 – 12x + 4 trên đoạn [−6; 3];
d) y = 2x3 – x2 – 28x – 3 trên đoạn [−2; 1];
e) y = −3x3 + 4x2 – 5x – 17 trên đoạn [−1; 2].
Bài 3 trang 17 SBT Toán 12 Tập 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) y = trên nửa khoảng (3; 4];
b) y = trên nửa khoảng ;
c) y = trên đoạn [0; 4].
Bài 5 trang 17 SBT Toán 12 Tập 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) y = ;
b) y = .
Bài 6 trang 17 SBT Toán 12 Tập 1
Một chất điểm chuyển động theo phương ngang có tọa độ xác định bởi phương trình x(t) = −0,01t4 + 0,12t3 + 0,3t2 + 0,5 với x tình bằng mét, t tính bằng giây, 0 ≤ t ≤ 6. Tìm thời điểm mà tốc độ của chất điểm lớn nhất.
Bài 7 trang 17 SBT Toán 12 Tập 1
Cho a và b là hai số không âm và có tổng bằng 4. Tìm giá trị nhỏ nhất của a4 + b4.
Bài 8 trang 18 SBT Toán 12 Tập 1
Từ một miếng bìa hình vuông có cạnh bằng 12 cm, người ta cắt bỏ đi bốn hình vuông nhỏ có cạnh bằng x (cm) ở bốn góc (Hình 3a) và gấp lại thành một hình hộp không nắp (Hình 3b). Tìm x để thể tích của hình hộp là lớn nhất.

Bài 9 trang 18 SBT Toán 12 Tập 1
Cho tam giác ABC cân tại A nội tiếp trong đường tròn tâm O, bán kính 1 cm. Đặt = α (0 < α < π).
a) Viết biểu thức tính diện tích S của tam giác ABC theo α.
b) Tìm diện tích lớn nhất của tam giác ABC.
Bài 10 trang 18 SBT Toán 12 Tập 1
Cho hình thang có đáy nhỏ và cạnh bên bằng nhau và bằng 5. Tìm diện tích lớn nhất của hình thang cân đó.
Bài 11 trang 18 SBT Toán 12 Tập 1
Trong một ngày, tổng chi phí để một xưởng sản xuất x (kg) thành phẩm được cho bởi hàm số C(x) = 2x3 – 30x2 + 177x + 2592 (nghìn đồng). Biết giá bán mỗi kilôgam thành phẩm là 513 nghìn đồng và công suất tối đa của xưởng 20 kg trong một ngày. Khối lượng thành phẩm xưởng nên sản xuất trong trong một ngày là bao nhiêu để lợi nhuận thu được của xưởng trong một ngày là cao nhất?
Bài 12 trang 18 SBT Toán 12 Tập 1
Giá bán P (đồng) của một sản phẩm thay đổi theo số lượng Q sản phẩm (0 ≤ Q ≤ 1 500) được cung cấp ra thị trường theo công thức P = . Tính số lượng sản phẩm nên được cung cấp ra thị trường để doanh thu R = PQ lớn nhất.