Giải bài tập Bài 23 trang 51 SBT Toán 12 Tập 2 | SBT Toán 12 - Kết nối tri thức (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 23 trang 51 SBT Toán 12 Tập 2. Bài tập ôn tập cuối năm. SBT Toán 12 - Kết nối tri thức (SBT)
Đề bài:
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số y = −x3 + 3x2 – 2.
b) Tìm điều kiện của tham số m để phương trình x3 – 3x2 + 5 – m = 0 có ba nghiệm phân biệt.
c) Tìm điểm thuộc đồ thị hàm số mà tiếp tuyến với đồ thị tại điểm có hệ số góc lớn nhất.
Đáp án và cách giải chi tiết:
a) Tập xác định: D = ℝ.
Ta có: y' = −3x2 + 6x
y' = 0 ⇔ x = 0 hoặc x = 2.
Ta có bảng biến thiên sau:
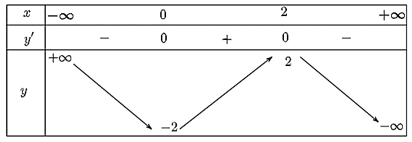
Hàm số đồng biến trên khoảng (0; 2).
Hàm số nghịch biến trên khoảng (−∞; 0) và (2; +∞).
Điểm cực đại và cực tiểu của hàm số lần lượt là (2; 2) và (0; −2).
Đồ thị hàm số nhận điểm uốn I(1; 0) làm tâm đối xứng.

b) Ta có: x3 – 3x2 + 5 – m = 0 ⇔ −x3 + 3x2 – 2 = 3 – m.
Vậy phương trình đã cho có ba nghiệm phân biệt khi và chỉ khi đường thẳng y = 3 – m cắt đồ thị y = −x3 + 3x2 – 2 tại ba điểm phân biệt.
Điều này tương đương với −2 < 3 – m < 2 ⇔ 1 < m < 5.
c) Ta có: y' = −3x2 + 6x = (−3x2 + 6x – 3) + 3 = −3(x – 1)2 + 3 ≤ 3, ∀x ∈ ℝ.
Vậy tiếp tuyến có hệ số góc lớn nhất bằng 3 tại x = 1.
Phương trình tiếp tuyến này là y = y'(1)(x – 1) + y(1)
⇔ y = 3(x – 1) + 0
⇔ y = 3x – 3.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 47 SBT Toán 12 Tập 2
Giá trị của tham số m để hàm số y = x3 – mx2 + 4x – 2023 đạt cực trị tại x = −2 là
A. Không tồn tại m.
B. m = −2.
C. m = 2.
D. m = 0.
Bài 2 trang 48 SBT Toán 12 Tập 2
Cho hàm số y = x3 + 3x2 + 1 có đồ thị (C). Xét đường thẳng đi qua điểm A(−3; 1) và có hệ số góc k. Điều kiện của k để đường thẳng đó cắt đồ thị (C) tại ba điểm phân biệt là
A. 0 < k < 1.
B. k > 0.
C. 1 < k < 9.
D. 0 < k ≠ 9.
Bài 3 trang 48 SBT Toán 12 Tập 2
Đồ thị trong hình vẽ dưới đây là của hàm số nào?

A.
B.
C.
D.
Bài 4 trang 48 SBT Toán 12 Tập 2
Tất cả các giá trị thực của tham số m để đường thẳng y = x + m – 1 cắt đồ thị hàm số y = tại hai điểm A, B thỏa mãn AB = là
A. m =
B. m =
C. m =
D. m =
Bài 5 trang 48 SBT Toán 12 Tập 2
Cho hàm số y = có đồ thị (C). Khẳng định nào sau đây là sai?
A. Đường thẳng x = −1 là tiệm cận đứng của đồ thị (C).
B. Đường thẳng y = 1 là tiệm cận ngang của đồ thị (C).
C. Đường thẳng y = x – 3 là tiệm cận xiên của đồ thị (C).
D. Hàm số có hai cực trị.
Bài 6 trang 49 SBT Toán 12 Tập 2
Cho f(x) là một hàm số liên tục trên đoạn [a; b] và F(x) là một nguyên hàm của f(x) trên [a; b]. Khi đó có giá trị bằng
A. F(b) – F(a).
B. F(b) – F(a) + C; C là hằng số.
C. F(a) – F(b).
D. F(a) – F(b) + C; C là hằng số.
Bài 7 trang 49 SBT Toán 12 Tập 2
Phát biểu nào sau đây là sai?
A. = x + C.
B. + C.
C. = lnx + C.
D. = ex + C.
Bài 8 trang 49 SBT Toán 12 Tập 2
Nguyên hàm F(x) của hàm số f(x) = 4x3 + 2x – 1 thỏa mãn F(1) = 10.
A. F(x) = x4 + x2 + 1.
B. F(x) = x4 – x2 + 10.
C. F(x) = x4 + x2 – x + 9.
D. F(x) = x4 + x2 – x + 10.
Bài 9 trang 49 SBT Toán 12 Tập 2
Cho và . Giá trị của là
A. 17.
B. 16.
C. 11.
D. 22.
Bài 10 trang 49 SBT Toán 12 Tập 2
Tích phân dùng để tính một trong các đại lượng sau, đó là đại lượng nào?
A. Diện tích hình phẳng giới hạn bởi các đường thẳng: y = (x – 1)2, y = 0, x = 1, x = 3.
B. Thể tích hình tròn xoay hình thành khi quay hình phẳng giới hạn bởi các đường: y = x – 1, y = 0, x = 1, x = 3 quanh trục Ox.
C. Diện tích hình phẳng giới hạn bởi các đường: y = (x – 1)2, y = 0, x = 2, x = 3.
D. Thể tích hình tròn xoay hình thành khi quay hình phẳng giới hạn bởi các đường: y = x – 1; y = 0, x = 2, x = 3 quanh trục Ox.
Bài 11 trang 50 SBT Toán 12 Tập 2
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = x2 + 2, y = 3x và các đường thẳng x = 1, x = 2 là
A. .
B. .
C. .
D. .
Bài 12 trang 50 SBT Toán 12 Tập 2
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC vuông cân tại B, biết SA = AB = BC = a. Gọi M là trung điểm của cạnh AC. Tính tích vô hướng bằng
A. .
B. a2.
C. −a2.
D. -.
Bài 13 trang 50 SBT Toán 12 Tập 2
Cho hình hộp ABCD.A'B'C'D', gọi G là trọng tâm của tam giác ADA' và M là trung điểm của đoạn thẳng CC'. Hệ thức biểu diễn theo ba vectơ là
A. .
B. .
C. .
D. .
Bài 14 trang 50 SBT Toán 12 Tập 2
Trong không gian Oxyz, cho đường thẳng ∆: . Một vectơ chỉ phương của đường thẳng ∆ là
A. = (3; −1; −4).
B. = (−4; −2; 6).
C. = (2; 1; 3).
D. = (3; 1; 4).
Bài 15 trang 50 SBT Toán 12 Tập 2
Trong không gian Oxyz, cho điểm A(2; −1; −3) và mặt phẳng (P): 2x – 2y – z = 0. Khoảng cách từ điểm A đến mặt phẳng (P) bằng
Bài 16 trang 50 SBT Toán 12 Tập 2
Trong không gian Oxyz, cho mặt cầu (S): x2+ y2 + z2 – 2x – 4y + 6z + 9 = 0. Tọa độ tâm I và bán kính R của mặt cầu (S) lần lượt là
A. I(1; 2; −3), R = 5.
B. I(1; 2; −3), R = .
C. I(2; 4; −6); R = 5.
D. I(2; 4; −6); R = .
Bài 17 trang 51 SBT Toán 12 Tập 2
Bảng tần số ghép nhóm sau cho biết thành tích luyện tập của một vận động viên nghiệp dư chạy maraton chạy 42 km.

Khoảng biến thiên của mẫu số liệu ghép nhóm là
A. 0,5.
B. 1,5.
C. 2,0.
D. 2,5.
Bài 18 trang 51 SBT Toán 12 Tập 2
Bảng tần số ghép nhóm sau cho biết thành tích luyện tập của một vận động viên nghiệp dư chạy maraton chạy 42 km.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là
A. 0,5.
B. 0,75.
C. 6,75.
D. 7,5.
Bài 19 trang 51 SBT Toán 12 Tập 2
Bảng tần số ghép nhóm sau cho biết thành tích luyện tập của một vận động viên nghiệp dư chạy maraton chạy 42 km.

Độ lệch chuẩn của mẫu số liệu ghép nhóm (làm tròn đến chữ số hàng phần trăm) là
A. 0,51.
B. 0,61.
C. 0,71.
D. 0,81.
Bài 20 trang 51 SBT Toán 12 Tập 2
Chọn ngẫu nhiên một lá bài từ cỗ bài tú lơ khơ gồm 52 lá bài. Xác suất để lá bài lấy ra có chất rô, nếu biết rằng lá bài đó mang số chẵn là
A. .
B. .
C. .
D. .