Giải bài tập Bài 1 trang 106 SBT Toán 12 Tập 1 | SBT Toán 12 - Chân trời sáng tạo (SBT)

Một tài xế ô tô công nghệ ở Thành phố Hồ Chí Minh đã thống kê khoảng cách của một số chuyến xe chạy trong địa phận thành phố ở bảng sau:

a) Khoảng biến thiên (đơn vị: km) của mẫu số liệu ghép nhóm trên là:

A. 50.

B. 10.

C. 40.

D. 30.

b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị nào sau đây?

A. 12,89.

B. 14,99.

C. 19,23.

D. 6,24.

c) Phương sai của mẫu số liệu ghép nhóm trên là

A. 104.

B. 21.

C. 10,2.

D. 441.

d) Độ lệch chuẩn của mẫu số liệu ghép nhóm trên gần nhất với giá trị nào sau đây?

A. 11,9.

B. 21.

C. 9,85.

D. 10,2.

Trong buổi tham quan vườn quốc gia Cát Tiên, nhóm học sinh lớp 12A3 đã ước lượng chiều dài thân của một số cá thể chuồn chuồn và ghi lại trong bảng số liệu sau:

a) Khoảng biến thiên (đơn vị: cm) của mẫu số liệu ghép nhóm trên là:

A. 6,5.

B. 5.

C. 4.

D. 7,5.

b) Nhóm chứa tứ phân vị thứ ba của mẫu số liệu trên là:

A. [3,5; 4,5).

B. [4,5; 5,5).

C. [5,5; 6,5).

D. [6,5; 7,5).

c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là:

A. 1,83.

B. 17,41.

C. 15,80.

D. 6,44.

d) Độ lệch chuẩn của mẫu số liệu ghép trên gần nhất với giá trị nào sau đây?

A. 1,29.

B. 5,13.

C. 2,27.

D. 1,14.

Chọn đúng hoặc sai cho mỗi ý a, b, c, d.

Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về cân nặng một số quả dưa được lựa chọn ngẫu nhiên từ một lô hàng:

a) Số phần tử của mẫu (cỡ mẫu) là n = 100.

b) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 80 g.

c) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là Q₃ = 830.

d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là ∆_Q = 29,6.

Biểu đồ dưới đây biểu diễn mẫu số liệu ghép nhóm mức lương nhân viên một công ty (đơn vị: triệu đồng).

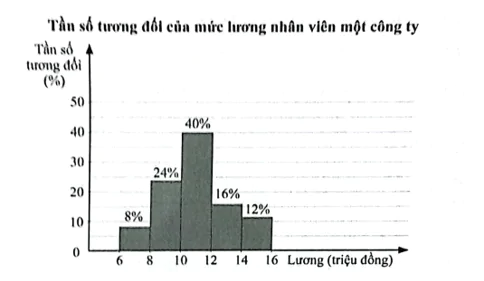
Biết công ty có 25 nhân viên.

Sử dụng biểu đồ trên, viết số thích hợp vào chỗ chấm trong các câu sau:

a) Tần số của nhóm [6; 8) là …..

b) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là ….. triệu đồng.

c) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là $\frac{\mathrm{a}}{12}$ với a bằng ….. 

d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là $\frac{\mathrm{b}}{24}$ với b bằng …… 

Một cây xăng thống kê lượng xăng bán được mỗi tuần ở bảng sau (đơn vị: m³):

a) Xác định phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).

b) Xác định khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).

c) Biết rằng có 1 tuần cửa hàng bán được 49 m³ xăng. Giá trị đó có phải là giá trị ngoại lệ không?

Người ta đo độ ẩm không khí lúc 12 giờ trưa mỗi ngày tại một địa điểm trong tháng 4. Kết quả các lần đo được biểu diễn ở biểu đồ tần số tương đối ghép nhóm dưới đây.

a) Hãy lập bảng tần số ghép nhóm cho dữ liệu ở biểu đồ trên.

b) Hãy tính các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm trên. (Làm tròn đến kết quả hàng phần trăm).

Nhiệt độ không khí trung bình hằng năm tại hai trạm quan trắc đạt ở Quy Nhơn và Cà Mau từ năm 2006 đến năm 2022 được ghi lại như sau:

a) Hãy chia dữ liệu trên thành 4 nhóm có độ dài bằng nhau với nhóm đầu tiên là [26,7; 27,1).

b) Hãy so sánh độ phân tán nhiệt độ không khí trung bình mỗi năm tại hai khu vực trên:

- theo khoảng biến thiên;

- theo khoảng tứ phân vị;

- theo phương sai.

Một nhóm nghiên cứu đã đo mức độ ồn của các phương tiện giao thông trên hai đường phố vào một ngày trong tuần, trong khoảng thời gian từ 5 giờ 30 phút đến 20 giờ 30 phút. Người ta đã thực hiện 92 lần đo ở mỗi con đường vào khoảng thời gian như nhau. Kết quả thống kê được ghi lại như trong bảng sau:

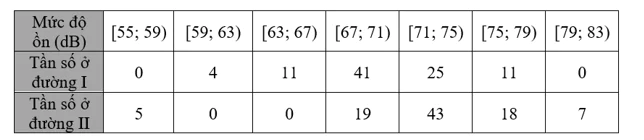
Hãy so sánh độ phân tán mức độ ồn của cá phương tiệm giao thông ở hai đường phố trên:

a) theo khoảng biến thiên;

b) theo khoảng tứ phân vị;

c) theo phương sai.

Độ tuổi của các kì thủ trong một giải cờ vua mở rộng được ghi lại trong bảng sau:

a) Hãy tính các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).

b) Biết rằng trong mẫu số liệu trên có một kì thủ 12 tuổi. Hỏi tuổi của kì thủ đó có là giá trị ngoại lệ không?

Bảng sau đây ghi lại khoảng thời gian hoàn thành đường bơi 500 m của một số học viên.

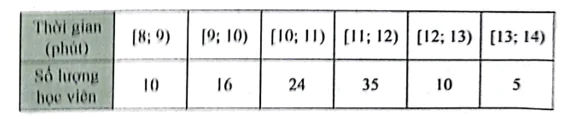
a) Xác định khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).

b) Xác định phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.

c) Xác định số giá trị ngoại lệ trong mẫu số liệu trên.