Tổng hợp bài tập có chứa công thức Công thức đạo hàm

Bài 6 trang 20 Toán 12 Tập 1: Người ta bơm xăng vào bình của một xe ô tô. Biết rằng thể tích V (lít) của lượng xăng trong bình xăng tính theo thời gian bơm xăng t (phút) được cho bởi công thức

$V\left(t\right) = 300(t^2 – t^3)+4 với 0 \le t \le 0,5$.    (Nguồn: R.I Charles et al., Algebra 2, Pearson)

a) Ban đầu trong bình xăng có bao nhiêu lít xăng?

b) Sau khi bơm 30 giây thì bình xăng đầy. Hỏi dung tích của bình xăng trong xe là bao nhiêu lít?

c) Khi xăng chảy vào bình xăng, gọi V'(t) là tốc độ tăng thể tích tại thời điểm t với 0 ≤ t ≤ 0,5. Xăng chảy vào bình xăng ở thời điểm nào có tốc độ tăng thể tích là lớn nhất?

Bài 5 trang 20 Toán 12 Tập 1: Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình $s\left(t\right)=-t^3+6t^2+t+5$,

trong đó t tính bằng giây và s tính bằng mét. Chất điểm có vận tốc tức thời lớn nhất bằng bao nhiêu trong 5 giây đầu tiên đó?

Bài 4 trang 20 Toán 12 Tập 1:  Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau:

a) $f\left(x\right)=x^3-\frac{3}{2}{x}^2$ trên đoạn [– 1; 2];

b) $f\left(x\right)=x^4-2x^3+x^2+1$ trên đoạn [– 1; 1];

c) $f\left(x\right) = e^x(x^2 – 5x + 7)$ trên đoạn [0; 3];

d) $f\left(x\right)=\cos \left(2x\right)+2x+1$ trên đoạn

Bài 3 trang 20 Toán 12 Tập 1: Tìm giá trị nhỏ nhất của mỗi hàm số sau:

a) $f\left(x\right)=x+\frac{4}{x}$ trên khoảng $\left(0;+\infty \right)$;          

b) $f\left(x\right)=x^3-12x+1$ trên khoảng $\left(1;+\infty \right)$.

Bài 2 trang 20 Toán 12 Tập 1: Tìm giá trị lớn nhất của mỗi hàm số sau:

a) $f\left(x\right)=\frac{4}{1+x^2}$;

b) $f\left(x\right)=x-\frac{3}{x}$ trên nửa khoảng (0; 3].

Bài 1 trang 19 Toán 12 Tập 1: Nếu hàm số $y=f\left(x\right)$ có đạo hàm trên ℝ thỏa mãn  $f\text{'}\left(x\right)=\sin \left(x\right)-2023$, $\forall x\in \mathrm{ℝ}$ thì giá trị lớn nhất của hàm số $y=f\left(x\right)$ trên đoạn [1; 2] bằng :

A. $f\left(0\right)$.

B. $f\left(1\right)$.

C. $f(1.5)$.

D. $f\left(2\right)$.

Bài 14 trang 38 Toán 12 Tập 1: Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b.

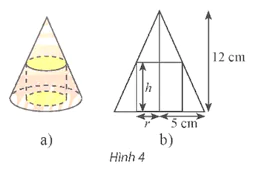
a) Chứng minh rằng công thức tính bán kính r của đáy hình trụ theo chiều cao h của nó là: $r = \frac{5\left(12 - h\right)}{12}.$

b) Chứng minh biểu thức sau biểu thị thể tích khối trụ theo h: $V\left(h\right) = \frac{25\mathrm{\pi h}{\left(12 - \mathrm{h}\right)}^2}{144}.$

Bài 13 trang 38 Toán 12 Tập 1: Cho hàm số $y = \frac{x^2 + 4x - 1}{x - 1}.$

a) Khảo sát và vẽ đồ thị của hàm số.

b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn $[2; 4].$

Bài 12 trang 38 Toán 12 Tập 1: Cho hàm số $y = \frac{2x + 1}{x - 1}.$

a) Khảo sát và vẽ đồ thị của hàm số.

b) Gọi A là giao điểm của đồ thị hàm số với trục Oy, I là giao điểm của hai đường tiệm cận của đồ thị hàm số. Tìm điểm B đối xứng với A qua I. Chứng minh rằng điểm B cũng thuộc đồ thị hàm số này.

Bài 4 trang 13 Toán 12 Tập 1:  Tìm điểm cực trị của mỗi hàm số sau:

a) $y=2x^3+3x^2-36x-10$;

b) $y=-x^4-2x^2+9$;

c) $y=x+\frac{1}{x}$.