Trang Chủ
Tổng hợp bài tập có chứa công thức Công thức đạo hàm

Tổng hợp bài tập có chứa công thức Công thức đạo hàm

Tổng hợp các bài tập cơ bản, nâng cao trong sách giáo khoa có ứng dụng công thức Công thức đạo hàm

Bài 1.10 trang 19 Toán 12 Tập 1

Bài 1.10 trang 19 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) y = −x² + 4x + 3;

b) y = x³ – 2x² + 1 trên [0; +∞);

c) $y = \frac{x^{2} - 2 x + 3}{x - 1}$ $y = \frac{x^{2} - 2 x + 3}{x - 1}$ trên (1; +∞);

d) $y = \sqrt{4 x - 2 x^{2}}$ .

Xem cách giải chi tiết

Bài 1.7 trang 14 Toán 12 Tập 1

Bài 1.7 trang 14 Toán 12 Tập 1: Tìm cực trị của các hàm số sau:

a) y = 2x³ – 9x² + 12x – 5;

b) y = x⁴ – 4x² + 2;

c) $y = \frac{x^{2} - 2 x + 3}{x - 1}$ ;

d) $y = \sqrt{4 x - 2 x^{2}}$ .

Xem cách giải chi tiết

Bài 1.4 trang 13 Toán 12 Tập 1

Bài 1.4 trang 13 Toán 12 Tập 1: Xét chiều biến thiên của các hàm số sau:

a) $y = \sqrt{4 - x^{2}}$ ;

b) $y = \frac{x}{x^{2} + 1}$ .

Xem cách giải chi tiết

Bài 1.3 trang 13 Toán 12 Tập 1

Bài 1.3 trang 13 Toán 12 Tập 1: Tìm các khoảng đơn điệu của các hàm số sau:

a) $y = \frac{2 x - 1}{x + 2}$

b) $y = \frac{x^{2} + x + 4}{x - 3}$

Xem cách giải chi tiết

Bài 1.2 trang 13 Toán 12 Tập 1

Bài 1.2 trang 13 Toán 12 Tập 1: Xét sự đồng biến, nghịch biến của các hàm số sau:

a) $y = \frac{1}{3} x^{3} - 2 x^{2} + 3 x + 1$ ;

b) y = −x³ + 2x² – 5x + 3.

Xem cách giải chi tiết

Bài 1.1 trang 13 Toán 12 Tập 1

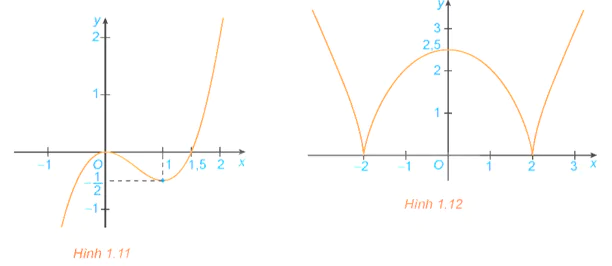
Bài 1.1 trang 13 Toán 12 Tập 1: Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:

a) Đồ thị hàm số (H.1.11);

b) Đồ thị hàm số (H.1.12).

Xem cách giải chi tiết

Bài 9 trang 47 Toán 12 Tập 1

Bài 9 trang 47 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

a) $y = x^{3} - 3 x^{2} + 2$ ;

b) $y = - x^{3} + 3 x^{2} - 6$ ;

c) $y = \frac{3 x - 2}{x - 2}$ ;

d) $y = \frac{x}{2 x + 3}$ ;

e) $y = \frac{x^{2} + 2 x + 4}{x}$ ;

g) $y = \frac{x^{2} + 4 x + 3}{x + 2}$ .

Xem cách giải chi tiết

Bài 6 trang 43 Toán 12 Tập 1

Bài 6 trang 43 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a) $y = \frac{x - 1}{x + 1}$ ;

b) $y = \frac{- 2 x}{x + 1}$ ;

c) $y = \frac{x^{2} - 3 x + 6}{x - 1}$ ;

d) $y = \frac{- x^{2} + 2 x - 4}{x - 2}$ ;

e) $y = \frac{2 x^{2} + 3 x - 5}{x + 2}$ ;

f) $y = \frac{x^{2} - 2 x - 3}{- x + 2}$

Xem cách giải chi tiết

Bài 8 trang 47 Toán 12 Tập 1

Bài 8 trang 47 Toán 12 Tập 1: Tìm giá trị nhỏ nhất và giá trị lớn nhất của mỗi hàm số sau:

a) $f (x) = 2 x^{3} - 6 x$ trên đoạn $[- 1; 3]$ ;

b) $f (x) = \frac{x^{2} + 3 x + 6}{x + 2}$ trên đoạn $[- 1; 3]$ ;

c) $f (x) = \frac{\ln (x + 1)}{x + 1}$ trên đoạn $[- 1; 3]$ ;

d) $f (x) = 2 \sin (3 x) + 7 x + 1$ trên đoạn $[- 1; 3]$ .

Xem cách giải chi tiết

Bài 5 trang 43 Toán 12 Tập 1

Bài 5 trang 43 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a) $y = 2 x^{3} - 3 x^{2} + 1$ ;

b) $y = - x^{3} + 3 x^{2} - 1$ ;

c) $y = {(x - 2)}^{3} + 4$ ;

d) $y = - x^{3} + 3 x^{2} - 3 x + 2$ ;

e) $y = \frac{1}{3} x^{3} + x^{2} + 2 x + 1$ ;

g) $y = - x^{3} - 3 x$ .

Xem cách giải chi tiết

Lời Giải Toán Phổ Thông

Toán 8

Toán 8 - Chân trời sáng tạo

Toán 8 - Kết nối tri thức

Toán 8 - Cánh diều

Toán 9

Toán 9 - Chân trời sáng tạo

Toán 9 - Kết nối tri thức

Toán 9 - Cánh diều

Toán 10

Toán 10 - Chân trời sáng tạo

Toán 10 - Kết nối tri thức

Toán 10 - Cánh diều

Toán 11

Toán 11 - Chân trời sáng tạo

Toán 11 - Kết nối tri thức

Toán 11 - Cánh diều

Chuyên đề học tập Chân Trời Sáng Tạo

Chuyên đề học tập Kết Nối Tri Thức

Chuyên đề học tập Cánh diều

Toán 12

SGK Toán 12 - Chân trời sáng tạo

SGK Toán 12 - Kết nối tri thức

SGK Toán 12 - Cánh diều

SBT Toán 12 - Chân trời sáng tạo (SBT)

SBT Toán 12 - Kết nối tri thức (SBT)

SBT Toán 12 - Cánh diều (SBT)

PDF Sách giáo khoa, Sách bài tập

Tài liệu tổng hợp Toán 12

Đề kiểm tra GK1

Đề kiểm tra CK1

Đề kiểm tra GK2

Đề kiểm tra CK2

Đề thi thử TN THPT QG

Từ điển Phương Trình Hoá Học

(NH4)2CO3 → H2O+NH3+CO2 HCl+Fe(OH)3 → H2O+FeCl3 H2+SO2 → H2O+S CuO+CH3-CH2-OH → Cu+H2O+CH3-CHO O2+CH3-CH2-OH → H2O+CH3-COOH

Công Thức Vật Lý

Công suất bức xạ. Định luật Ohm cho mạch chỉ chứa L - Vật lý 12 Hai giá trị R cùng dòng điện và mối liên hệ đến công suất cực đại - Vật lý 12