Giải bài tập Bài 12 trang 12 SBT Toán 12 Tập 1 | SBT Toán 12 - Chân trời sáng tạo (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 12 trang 12 SBT Toán 12 Tập 1. Bài 1. Tính đơn điệu và cực trị của hàm số. SBT Toán 12 - Chân trời sáng tạo (SBT)
Đề bài:
Cho điểm A di động trên nửa đường tròn tâm O đường kính MN = 20 cm, = α với 0 ≤ α ≤ π. Lấy điểm B thuộc nửa đường tròn và C, D thuộc đường kính MN được xác định sao cho ABCD là hình chữ nhật. Khi A di động từ trái sang phải, trong các khoảng nào của α thì diện tích của hình chữ nhật ABCD tăng, trong khoảng nào của α thì diện tích hình chữ nhật ABCD giảm?
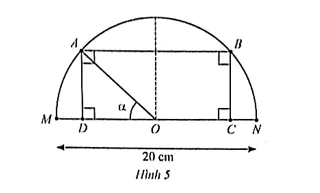
Đáp án và cách giải chi tiết:
Xét tam giác ADO vuông tại D, có AD = sin.AO = 10sinα;
DO = cos.AO = 10cosα.
Diện tích hình chữ nhật ABCD là: y = AD.DC = AD.2DO = 200sinαcosα = 100sin2α.
Ta có: y' = 200cos2α
y' = 0 ⇔ α = (0 ≤ α ≤ π).
Ta có bảng biến thiên:
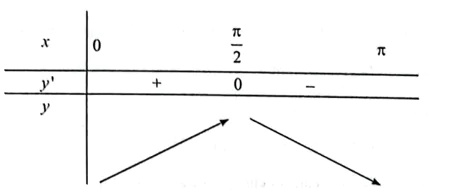
Diện tích ABCD tăng trên khoảng , giảm trên khoảng .
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 10 SBT Toán 12 Tập 1
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 3.

Bài 2 trang 10 SBT Toán 12 Tập 1
Xét tính đơn điệu và tìm cực trị của các hàm số:
a) y = −x3 – 3x2 + 24x – 1;
b) y = x3 – 8x2 + 5x + 2;
c) y = x3 + 2x2 + 3x + 1;
d) y = −3x3 + 3x2 – x + 2.
Bài 3 trang 10 SBT Toán 12 Tập 1
Xét tính đơn điệu và tìm cực trị của các hàm số:

Bài 4 trang 10 SBT Toán 12 Tập 1
Xét tính đơn điệu và tìm cực trị của các hàm số:
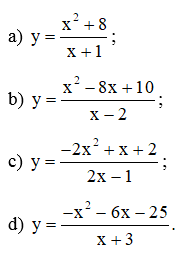
Bài 5 trang 10 SBT Toán 12 Tập 1
Tìm m để
a) Hàm số y = đồng biến trên từng khoảng xác định.
b) Hàm số y = nghịch biến trên từng khoảng xác định.
Bài 6 trang 11 SBT Toán 12 Tập 1
Đạo hàm f'(x) của hàm số y = f(x) có đồ thị như Hình 4. Xét tính đơn điệu và tìm các điểm cực trị của hàm số y = f(x).

Bài 7 trang 11 SBT Toán 12 Tập 1
Chứng minh rằng:
a) tanx ≥ x với mọi x ∈ .
b) lnx ≤ x – 1 với mọi x > 0.
Bài 8 trang 11 SBT Toán 12 Tập 1
Chứng minh rằng:
a) Phương trình x3 + 5x2 – 8x + 4 = 0 có duy nhất một nghiệm.
b) Phương trình −x3 + 3x2 + 24x – 1 = 0 có ba nghiệm phân biệt.
Bài 9 trang 11 SBT Toán 12 Tập 1
Tìm m để phương trình có hai nghiệm phân biệt.
Bài 10 trang 11 SBT Toán 12 Tập 1
Một chất điểm chuyển động lên, xuống theo phương thẳng đứng. Độ cao h(t) của chất điểm tại thời điểm t (giây) được cho bởi công thức
h(t) = t3 – 4t2 + 12t + 1 với 0 ≤ t ≤ 8.
a) Viết công thức tính vận tốc của chất điểm.
b) Trong khoảng thời gian nào chất điểm chuyển động lên, trong khoảng thời gian nào chất điểm chuyển động đi xuống?
Bài 11 trang 11 SBT Toán 12 Tập 1
Độ cao (tính bằng mét) của tàu lượn siêu tốc so với mặt đất sau t (giây) (0 ≤ t ≤ 20) từ lúc bắt đầu được cho bởi công thức
h(t) = .
Trong khoảng thời gian nào tàu lượn đi xuống, trong khoảng thời gian nào thời gian tàu lượn đi lên?
Bài 13 trang 12 SBT Toán 12 Tập 1
Người ta thấy rằng trong vòng 3 năm tính từ đầu năm 2020, giá thành P của một loại sản phẩm vào tháng thứ t thay đổi theo công thức
P(t) = 80t3 – 3600t2 + 48 000t + 100 000 (đồng) với 0 ≤ t ≤ 36.
Hãy cho biết trong khoảng thời gian nào giá thành sản phẩm tăng, trong khoảng thời gian nào giá thành sản phẩm giảm. Giá thành đạt cực đại và cực tiểu vào thời điểm nào?
Bài 14 trang 12 SBT Toán 12 Tập 1
Một cửa hàng ước tính số lượng sản phẩm q (0 ≤ q ≤ 100) bán được phụ thuộc vào giá bán p (tính bằng nghìn đồng) theo công thức p + 2q = 300. Chi phi cửa hàng cần chi để nhập về q sản phẩm là C(p) = 0,05p3 – 5,7q2 + 295q + 300 (nghìn đồng).
a) Viết công thức tính lợi nhuận l của cửa hàng khi nhập về và bán được q sản phẩm.
b) Trong khoảng nào của q thì lợi nhuận sẽ tăng khi q tăng, trong khoảng nào thì lợi nhuận giảm khi q tăng?