Tổng hợp bài tập có chứa công thức Công thức đạo hàm
Tổng hợp các bài tập cơ bản, nâng cao trong sách giáo khoa có ứng dụng công thức Công thức đạo hàm
Bài 9.26 trang 98 Toán 11 Tập 2
Xét hàm số lũy thừa y = xα với α là số thực.
a) Tìm tập xác định của hàm số đã cho.
b) Bằng cách viết y = xα = eαlnx, tính đạo hàm của hàm số đã cho.
Bài 9.25 trang 97 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau:
a) 
;
b)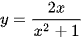 
;
c) y = exsin2x;
d) 
.
Bài 9.24 trang 97 Toán 11 Tập 2
Cho hàm số y = x3 – 3x2 + 4x – 1 có đồ thị là (C). Hệ số góc nhỏ nhất của tiếp tuyến tại một điểm M trên đồ thị (C) là
A. 1.
B. 2.
C. –1.
D. 3.
Bài 9.23 trang 97 Toán 11 Tập 2
Chuyển động của một vật có phương trình , ở đó s tính bằng centimét và thời gian t tính bằng giây. Tại các thời điểm vận tốc bằng 0, giá trị tuyệt đối của gia tốc của vật gần với giá trị nào sau đây nhất?
A. 4,5 cm/s2.
B. 5,5 cm/s2.
C. 6,3 cm/s2.
D. 7,1 cm/s2.
Bài 9.22 trang 97 Toán 11 Tập 2
Cho hàm số f(x) = x2e–2x. Tập nghiệm của phương trình f'(x) = 0 là
A. {0; 1}.
B. {–1; 0}.
C. {0}.
D. {1}.
Bài 9.21 trang 97 Toán 11 Tập 2
Cho hàm số 
với u(1) = 7, u'(1) = 10. Khi đó f'(1) bằng
A. 1.
B. 6.
C. 3.
D. –3.
Bài 9.20 trang 97 Toán 11 Tập 2
Cho hàm số . Tập nghiệm của bất phương trình f'(x) ≤ 0 là
A. [1; 3].
B. [–1; 3].
C. [–3; 1].
D. [–3; –1].
Bài 9.19 trang 97 Toán 11 Tập 2
Cho hàm số f(x) = x2 + sin3x. Khi đó bằng
A. π.
B. 2π.
C. π + 3.
D. π – 3.
Bài 9.18 trang 97 Toán 11 Tập 2
Với u, v là các hàm số hợp theo biến x, quy tắc tính đạo hàm nào sau đây là đúng?
A. (u + v)' = u' – v'.
B. (uv)' = u'v + uv'.
C.
D.
Bài 9.17 trang 96 Toán 11 Tập 2
Phương trình chuyển động của một hạt được cho bởi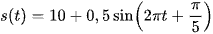 
, trong đó s tính bằng centimet và t tính bằng giây. Tính gia tốc của hạt tại thời điểm t = 5 giây (làm tròn kết quả đến chữ số thập phân thứ nhất).