Tổng hợp bài tập có chứa công thức Công thức đạo hàm
Tổng hợp các bài tập cơ bản, nâng cao trong sách giáo khoa có ứng dụng công thức Công thức đạo hàm
Bài 4 trang 75 Toán 11 Tập 2
Một chất điểm chuyển động theo phương trình s(t) = t3 – 3t2 + 8t + 1, trong đó t > 0, t tính bằng giây và s(t) tính bằng mét. Tính vận tốc tức thời, gia tốc tức thời của chất điểm:
a) Tại thời điểm t = 3 (s);
b) Tại thời điểm mà s(t) = 7 (m)
Bài 3 trang 75 Toán 11 Tập 2
Một vật rơi tự do theo phương thẳng đứng có phương trình chuyển động trong đó g là gia tốc rơi tự do, g ≈ 9,8 m/s2.
a) Tính vận tốc tức thời của vật tại thời điểm t0 = 2 (s).
b) Tính gia tốc tức thời của vật tại thời điểm t0 = 2 (s).
Bài 2 trang 75 Toán 11 Tập 2
Tính đạo hàm cấp hai của mỗi hàm số sau:
a) y = 3x2 – 4x + 5 tại điểm x0 = –2;
b) y = log3(2x + 1) tại điểm x0 = 3;
c) y = e4x + 3 tại điểm x0 = 1;
d) 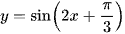 tại điểm
tại điểm 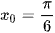 ;
;
e) 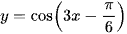 tại điểm x0 = 0.
tại điểm x0 = 0.
Bài 1 trang 75 Toán 11 Tập 2
Tìm đạo hàm cấp hai của mỗi hàm số sau:
a) 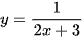 ;
;
b) y = log3x;
c) y = 2x.
Bài 8 trang 72 Toán 11 Tập 2
Cho mạch điện như Hình 5. Lúc đầu tụ điện có điện tích Q0. Khi đóng khóa K, tụ điện phóng điện qua cuộn dây; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức q(t) = Q0sinωt, trong đó ω là tốc độ góc. Biết rằng cường độ I(t) của dòng điện tại thời điểm t được tính theo công thức I(t) = q'(t). Cho biết Q0 = 10–8 (C) và ω = 106π (rad/s). Tính cường độ dòng điện tại thời điểm t = 6 (s) (tính chính xác đến 10–5 mA)
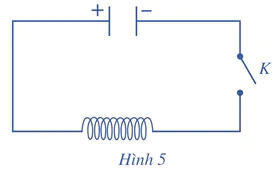
Bài 7 trang 72 Toán 11 Tập 2
Một viên đạn được bắn từ mặt đất theo phương thẳng đứng với tốc độ ban đầu v0 = 196 m/s (bỏ qua sức cản của không khí). Tìm thời điểm mà tốc độ của viên đạn bằng 0. Khi đó viên đạn cách mặt đất bao nhiêu mét (lấy g = 9,8 m/s2)?
Bài 6 trang 72 Toán 11 Tập 2
Viết phương trình tiếp tuyến của đồ thị mỗi hàm số sau:
a) y = x3 – 3x2 + 4 tại điểm có hoành độ x0 = 2;
b) y = lnx tại điểm có hoành độ x0 = e;
c) y = ex tại điểm có hoành độ x0 = 0.
Bài 5 trang 72 Toán 11 Tập 2
Tìm đạo hàm của mỗi hàm số sau:
a) y = sin3x + sin2x
b) y = log2(2x + 1) + 3−2x + 1
Bài 4 trang 71 Toán 11 Tập 2
Cho hàm số f(x) = 23x + 2.
a) Hàm số f(x) là hàm hợp của các hàm số nào?
b) Tìm đạo hàm của f(x)
Bài 3 trang 71 Toán 11 Tập 2
Tìm đạo hàm của mỗi hàm số sau:
a) y = 4x3 – 3x2 + 2x + 10;
b) 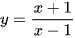 ;
;
c) 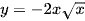 ;
;
d) y = 3sinx + 4cosx – tanx;
e) y = 4x + 2ex;
g) y = xlnx