Tổng hợp bài tập có chứa công thức Công thức đạo hàm

Bài 3 trang 49 Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:

a) y = (x² – x)×2^x;

b) y = x²log₃x;

c) y = e^{3x + 1}.

Bài 2 trang 49 Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:

a) y = sin3x;

b) y = cos³2x;

c) y = tan²x;

d) y = cot(4 – x²).

Bài 1 trang 48 Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:

a) ;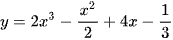

b) ;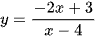

c) ;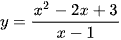

d) .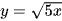

Bài 6 trang 42 Toán 11 Tập 2: Trên Mặt Trăng, quãng đường rơi tư do của một vật được cho bởi công thức h(t) = 0,81t², với được tính bằng giây và tính bằng mét. Hãy tính vận tốc tức thời của vật được thả rơi tự do trên Mặt Trăng tại thời điểm t = 2.

Bài 3 trang 42 Toán 11 Tập 2: Viết phương trình tiếp tuyến của đồ thị hàm số y = x³.

a) Tại điểm (−1; 1);

b) Tại điểm có hoành độ bằng 2.

Bài 2 trang 41 Toán 11 Tập 2: Cho hàm số f(x) = −2x² có đồ thị (C) và điểm A(1; −2) ∈ (C). Tính hệ số góc của tiếp tuyến với (C) tại điểm A.

Bài 1 trang 41 Toán 11 Tập 2: Dùng định nghĩa để tính đạo hàm của các hàm số sau:

a) f(x) = −x²;

b) f(x) = x² − 2x;

c) $\mathrm{f}\left(\mathrm{x}\right)=\frac{4}{\mathrm{x}}$

Bài 7 trang 25 Toán 11 Tập 2: Công thức $\mathrm{h}=-19,4.\log \frac{\mathrm{P}}{{\mathrm{P}}_0}$ là mô hình đơn giản cho phép tính độ cao h so với mặt nước biển của một vị trí trong không trung (tính bằng kilômét) theo áp suất không khí P tại điểm đó và áp suất P₀ của không khí tại mặt nước biển (cùng tính bằng Pa – đơn vị áp suất, đọc là Pascal).

(Nguồn: https://doi.org/10.1007/s40828-020-0111-6)

a) Nếu áp suất không khí ngoài máy bay bằng $\frac{1}{2}{\mathrm{P}}_0$ thì máy bay đang ở độ cao nào?

b) Áp suất không khí tại đỉnh của ngọn núi A bằng $\frac{4}{5}$ lần áp suất không khí tại đỉnh của ngọn núi B. Ngọn núi nào cao hơn và cao hơn bao nhiêu kilômét? (Làm tròn kết quả đến hàng phần mười.)

Bài 6 trang 25 Toán 11 Tập 2: Cường độ ánh sáng I dưới mặt biển giảm dần theo độ sâu theo công thức I = I₀.a^d, trong đó I₀ là cường độ ánh sáng tại mặt nước biển, a là hằng số (a > 0) và d là độ sâu tính bằng mét tính từ mặt nước biển.

(Nguồn: https://www.britannica.com/science/seawer/Optical-properties)

a) Có thể khẳng định rằng 0 < a < 1 không? Giải thích.

b) Biết rẳng cường độ ánh sáng tại độ sâu 1 m bằng 0,95I₀. Tìm giá trị của a.

c) Tại độ sâu 20 m, cường độ ánh sáng bằng bao nhiêu phần trăm so với I₀? (Làm tròn kết quả đến hàng đơn vị.)

Bài 5 trang 25 Toán 11 Tập 2: So sánh các cặp số sau:

a) log_π 0,8 và log_π 1,2;    

b) log_0,3 2 và log_0,3 2,1.