Cách xác định số điểm cực trị của hàm số chứa dấu giá trị tuyệt đối dựa trên công thức tính nhanh | SGK Toán 12 - Cánh diều
Cách xác định số điểm cực trị của hàm số chứa dấu giá trị tuyệt đối dựa trên công thức tính nhanh
Dưới đây là công thức Cách xác định số điểm cực trị của hàm số chứa dấu giá trị tuyệt đối dựa trên công thức tính nhanh
Nhận xét:
Số điểm cực trị của hàm số |f(x)| bằng tổng số điểm cực trị của hàm số f(x) và số nghiệm đơn và bội lẻ của phương trình f(x) = 0. Hay cách khác bằng tổngsố điểm cực trị của hàm số f(x).
Số điểm cực trị của hàm số f(|x|) bằng 2a + 1, trong đó a là số điểm cực trị dương của hàm số f(x).
Đặc biệt với hàm số 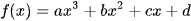 có hai điểm cực trị
có hai điểm cực trị 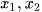 . Khi đó hàm số y = |f(x)| có n điểm cực trị
. Khi đó hàm số y = |f(x)| có n điểm cực trị
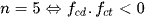 và tương đương với f(x) = 0 có 3 nghiệm thực phân biệt
và tương đương với f(x) = 0 có 3 nghiệm thực phân biệt
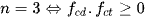 .
.
Ví dụ 1: Cho hàm số 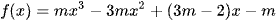 . Số giá trị nguyên của tham số m ∈ [-10; 10] để hàm số g(x) = |f(x) + 2| có 5 điểm cực trị là
. Số giá trị nguyên của tham số m ∈ [-10; 10] để hàm số g(x) = |f(x) + 2| có 5 điểm cực trị là
A. 10.
B. 11.
C. 9.
D. 7.
Lời giải
Ta có ycbt ⇔ f(x) + 2 = 0 ⇔ 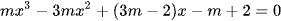
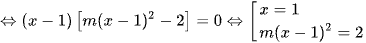 có 3 nghiệm phân biệt ⇔ m > 0 ⇒ m ∈ {1; ...; 10}.
có 3 nghiệm phân biệt ⇔ m > 0 ⇒ m ∈ {1; ...; 10}.
Chọn đáp án A.
Ví dụ 2: Cho hàm số 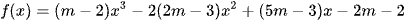 . Số giá trị nguyên dương của tham số m để hàm số g(x) = |f(x)| có 5 điểm cực trị là
. Số giá trị nguyên dương của tham số m để hàm số g(x) = |f(x)| có 5 điểm cực trị là
A. 3.
B. 2.
C. 0.
D. 1.
Lời giải
Ta có ycbt ⇔ f(x) = 0 ⇔ 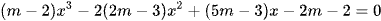
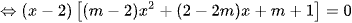
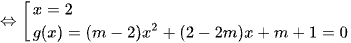 có 3 nghiệm phân biệt.
có 3 nghiệm phân biệt.
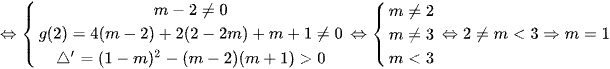 .
.
Chọn đáp án D.
Ví dụ 3: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số 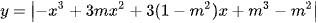 có 5 điểm cực trị. Tổng các phần tử của S bằng
có 5 điểm cực trị. Tổng các phần tử của S bằng
A. -2.
B. 3.
C. 7.
D. 4.
Lời giải
Ta có ycbt ⇔ 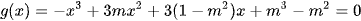 có 3 nghiệm phân biệt (*)
có 3 nghiệm phân biệt (*)
Ta có 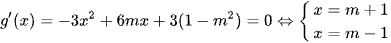 .
.
Vậy (*) 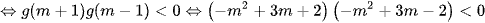
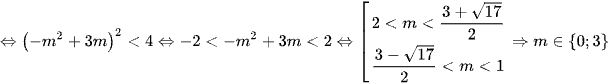 .
.
Chọn đáp án B.
Các bài toán biện luận số điểm cực trị của hàm tuyệt đối dạng |u(x)| ta đưa về xét dấu đồng thời của u(x) và u'(x).
Chi tiết xem ví dụ:
Ví dụ 1: Có bao nhiêu giá trị nguyên của tham số m ∈ [-200; 200] để hàm số 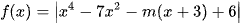 có đúng 3 điểm cực trị?
có đúng 3 điểm cực trị?
Lời giải
Xét 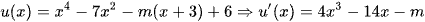 .
.
Ta có bảng biến thiên của g(x), h(x) như sau:
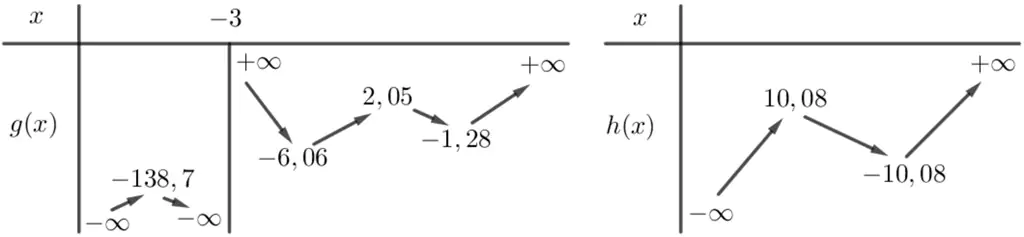
Hàm số f(x) = |u(x)| có đúng 3 điểm cực trị khi và chỉ khi
TH1: u'(x) có 1 lần đổi dấu và u(x) có 2 lần đổi dấu ⇒ m ∈ {-200; ...; -139; 11; ...; 200}.
TH2: u'(x) có 3 lần đổi dấu và u(x) có 0 lần đổi dấu ⇒ m ∈ {-10; ...; -7}.
Vậy m ∈ {-200; ...; -139; -10; ...; -7; 11; ...; 200}. Có tất cả (-139 - (-200) + 1) + (-7 - (-10) + 1) + (200 - 11 + 1) = 256 giá trị nguyên của m ∈ [-200; 200] thoả mãn.
Chọn đáp án D.
Ví dụ 2: Cho hàm số 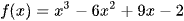 . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 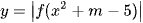 có ít nhất 7 điểm cực trị?
có ít nhất 7 điểm cực trị?
A. 7.
B. 6.
C. 3.
D. 8.
Lời giải
Ta có 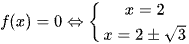 và
và 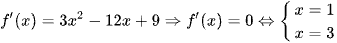 .
.
Xét 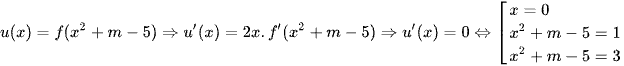 .
.
Và 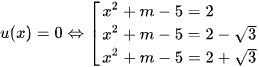 .
.
Hàm số 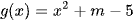 có bảng biến thiên như sau:
có bảng biến thiên như sau:
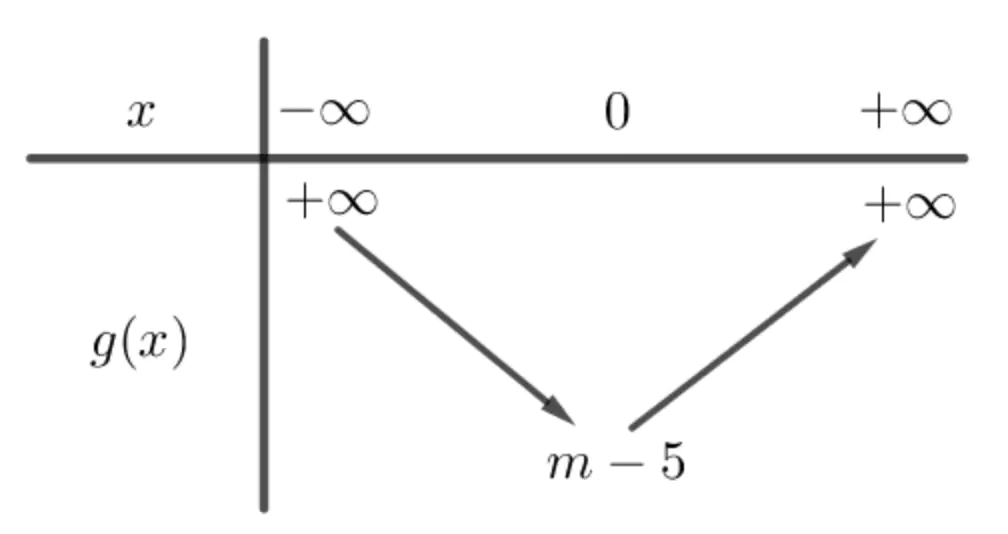
Ta cần tìm điều kiện để tổng số lần đổi dấu của u(x) và u'(x) ít nhất bằng 7.
Tức tổng số lần đổi dấu của 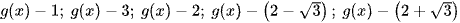 ít nhất bằng 6.
ít nhất bằng 6.
Vậy m - 5 < 2 ⇔ m < 7 ⇒ m ∈ {1; ...; 6}.
Chọn đáp án B.