Tổng hợp tất cả các công thức tính nhanh hay được sử dụng chương Nguyên hàm và tích phân | SGK Toán 12 - Cánh diều
Tổng hợp tất cả các công thức tính nhanh hay được sử dụng chương Nguyên hàm và tích phân
Dưới đây là công thức Tổng hợp tất cả các công thức tính nhanh hay được sử dụng chương Nguyên hàm và tích phân
A - TÌM NGUYÊN HÀM VÀ TÍNH TÍCH PHÂN
DẠNG 1: TÍNH CHẤT TÍCH PHÂN DỰA TRÊN CẬN VÀ PHÉP ĐỔI BIẾN SỐ
A – Với y = f(x) là hàm liên tục trên đoạn [a; b], ta có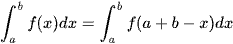 
, phép đổi biến x = a + b - t.
Do đó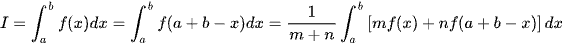 
.
B – Với f(x) là hàm số lẻ, liên tục trên đoạn [-a; a], tức f(-x) = -f(x), ta có
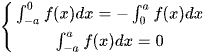
Chứng minh:
Đổi biến x = -t ⇒ dx = -dt; x = -a ⇒ t = a; x = 0 ⇒ t = 0. Khi đó,
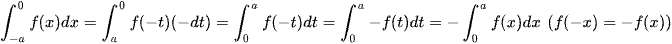
và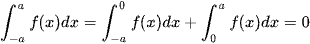 
.
C – Với f(x) là hàm chẵn, liên tục trên đoạn [-a; a], tức f(-x) = f(x), ta có
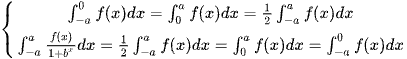
Chứng minh:
Đổi biến x = -t ⇒ dx = -dt; x = -a ⇒ t = a; x = 0 ⇒ t = 0. Khi đó,
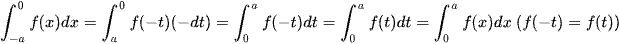
và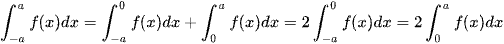 
.
Xét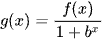 
khi đó theo tính chất tích phân dựa trên phép đổi biến có:
.
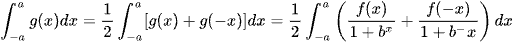
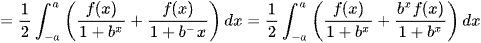
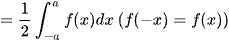D – Với f(x) là hàm tuần hoàn chu kì T, liên tục trên R tức f(x + T) = f(x), ta có
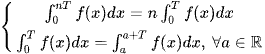
Chứng minh:
Tách tích phân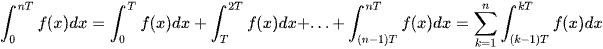 
.
Đổi biến x = t + (k - 1)T ⇒ dx = dt; x = (k - 1)T ⇒ t = 0; x = kT ⇒ t = T.
Khi đó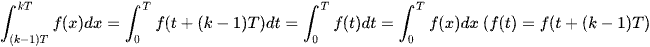 
.
Vậy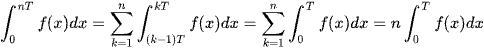 
.
Tính chất tiếp theo tách thành tổng các tích phân: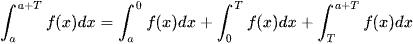 
.
Đổi biến x = t + T ⇒ dx = dt; x = T ⇒ t = 0; x = a + T ⇒ t = a.
Khi đó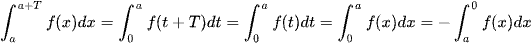 
.
Suy ra điều phải chứng minh.
DẠNG 2: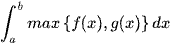 
VÀ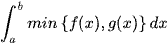 
;
.
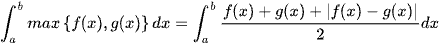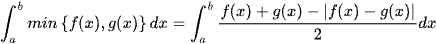B - ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH HÌNH PHẲNG, THỂ TÍCH VẬT THỂ