3 công thức tính nhanh diện tích hình phẳng hay bậc nhất trong chương Nguyên hàm và tích phân | SGK Toán 12 - Cánh diều
3 công thức tính nhanh diện tích hình phẳng hay bậc nhất trong chương Nguyên hàm và tích phân
Dưới đây là công thức 3 công thức tính nhanh diện tích hình phẳng hay bậc nhất trong chương Nguyên hàm và tích phân
CÔNG THỨC 1: DIỆN TÍCH HÌNH PHẲNG GIỚI HẠN BỞI PARABOL VÀ ĐƯỜNG THẲNG
Khi đường thẳng y = mx + n cắt parabol 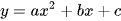 tại hai điểm phân biệt, tính diện tích hình phẳng giới hạn bởi hai đường đã cho
tại hai điểm phân biệt, tính diện tích hình phẳng giới hạn bởi hai đường đã cho
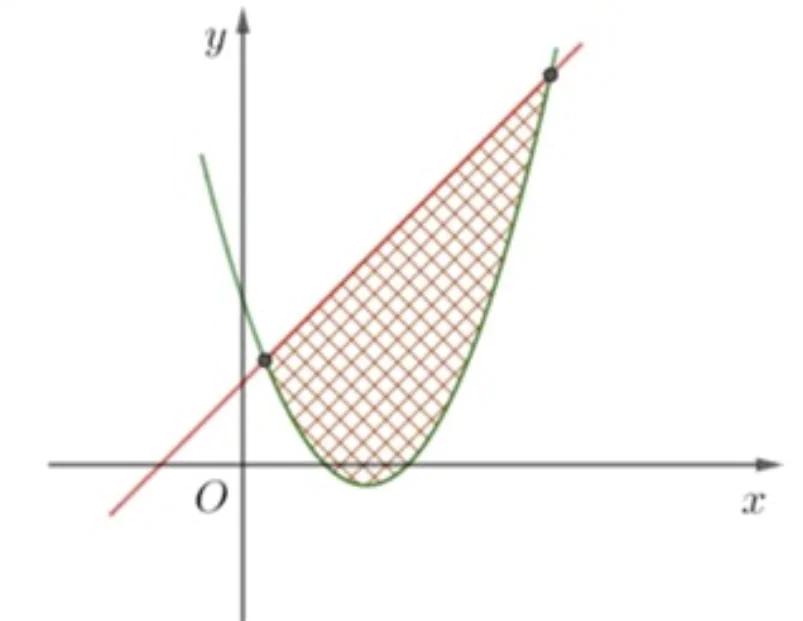
Xét phương trình hoành độ giao điểm: 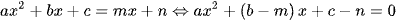 .
.
Khi đó diện tích hình phẳng giới hạn bởi đường cong parabol và đường thẳng xác định bởi công thức
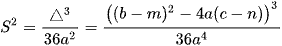 .
.
Ví dụ áp dụng: Xét hai điểm A, B phân biệt trên parabol (P): 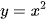 sao cho
sao cho 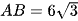 . Giá trị lớn nhất của diện tích hình phẳng giới hạn bởi (P) và đường thẳng AB bằng
. Giá trị lớn nhất của diện tích hình phẳng giới hạn bởi (P) và đường thẳng AB bằng
A. 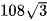
B. 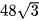
C. 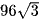
D. 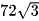
Lời giải
Gọi A(a; 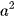 ); B(b;
); B(b; 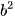 ).
).
Phương trình đường thẳng qua hai điểm A, B là 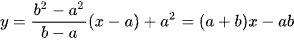 .
.
Phương trình hoành độ giao điểm: 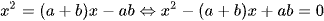 .
.
Diện tích hình phẳng giới hạn bởi (P) và đường thẳng AB là 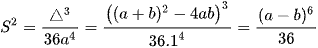 .
.
Vì\ 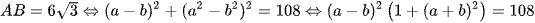 .
.
Do đó 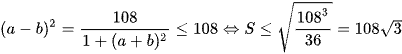 .
.
Chọn đáp án A.
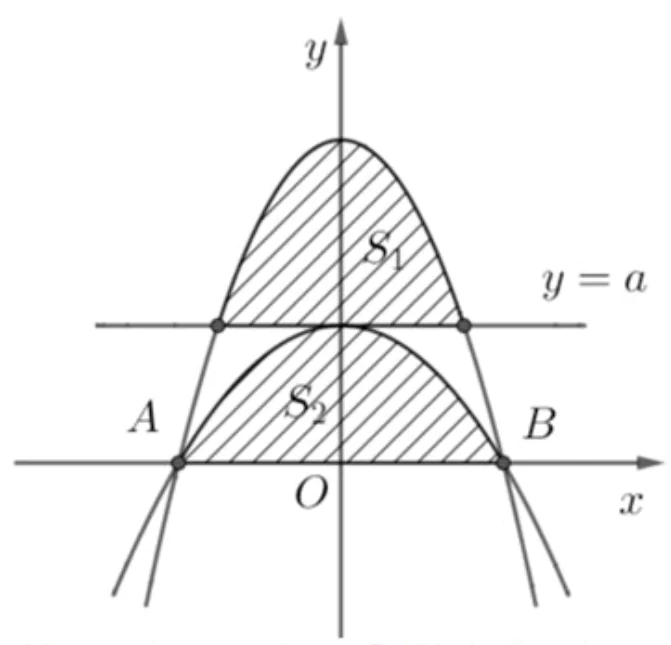
Câu 57: Cho parabol 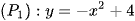 cắt trục hoành tại hai điểm phân biệt A, B và đường thẳng d: y = a (0 < a < 4). Xét parabol
cắt trục hoành tại hai điểm phân biệt A, B và đường thẳng d: y = a (0 < a < 4). Xét parabol 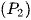 có đỉnh thuộc đường thẳng d và đi qua hai điểm A, B. Gọi
có đỉnh thuộc đường thẳng d và đi qua hai điểm A, B. Gọi 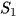 là diện tích hình phẳng giới hạn bởi
là diện tích hình phẳng giới hạn bởi 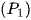 và đường thẳng d;
và đường thẳng d; 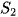 là diện tích hình phẳng giới hạn bởi
là diện tích hình phẳng giới hạn bởi 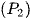 và trục hoành. Biết rằng
và trục hoành. Biết rằng 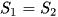 . Giá trị của
. Giá trị của 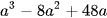 bằng
bằng
A. 96
B. 64
C. 72
D. 32
Lời giải
Có 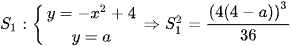 .
.
Có 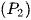 qua các điểm A(-2; 0); B(2; 0); I(0; a)
qua các điểm A(-2; 0); B(2; 0); I(0; a) 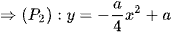 .
.
Vậy 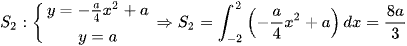 .
.
Vậy 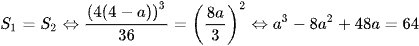 .
.
Chọn đáp án B.
CÔNG THỨC 2: DIỆN TÍCH HÌNH PHẲNG GIỚI HẠN BỞI ĐƯỜNG CONG BẬC BA VÀ ĐƯỜNG THẲNG
Khi đường thẳng y = mx + n cắt đường cong bậc ba 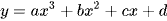 tại ba điểm phân biệt và hình phẳng giới hạn bởi hai đường này gồm phần phía trên và phía dưới đường thẳng có diện tích bằng nhau khi và chỉ khi điểm uốn
tại ba điểm phân biệt và hình phẳng giới hạn bởi hai đường này gồm phần phía trên và phía dưới đường thẳng có diện tích bằng nhau khi và chỉ khi điểm uốn 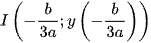 của đường cong bậc ba thuộc đường thẳng y = mx + n.
của đường cong bậc ba thuộc đường thẳng y = mx + n.
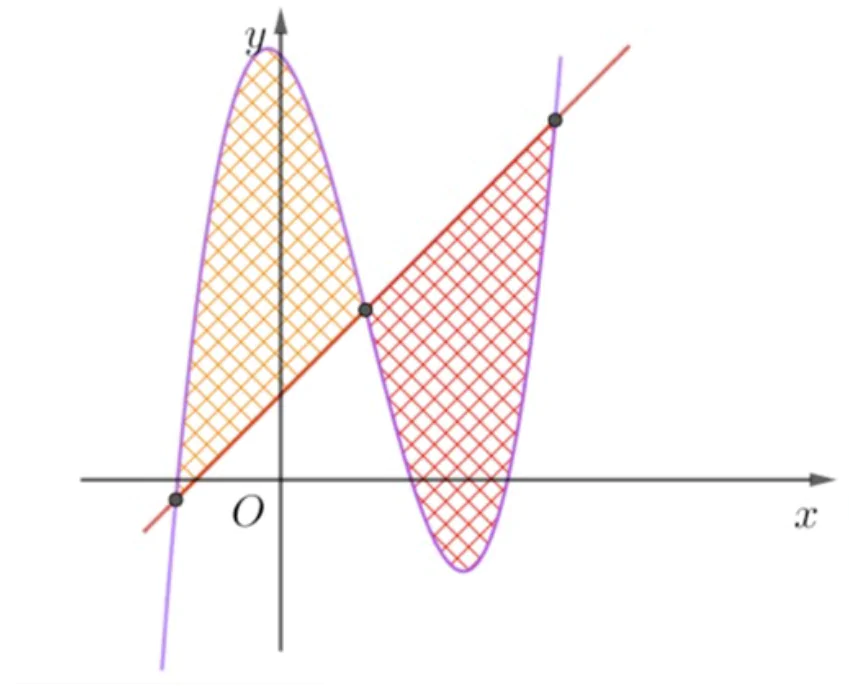
CÔNG THỨC 3: DIỆN TÍCH HÌNH PHẲNG GIỚI HẠN BỞI ĐƯỜNG CONG TRÙNG PHƯƠNG VÀ ĐƯỜNG THẲNG
Khi đường thẳng y = m cắt đường cong trùng phương 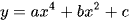 tại bốn điểm phân biệt và hình phẳng giới hạn bởi hai đường này gồm phần phía trên và phía dưới đường thẳng có diện tích bằng nhau khi và chỉ khi
tại bốn điểm phân biệt và hình phẳng giới hạn bởi hai đường này gồm phần phía trên và phía dưới đường thẳng có diện tích bằng nhau khi và chỉ khi 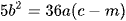 .
.
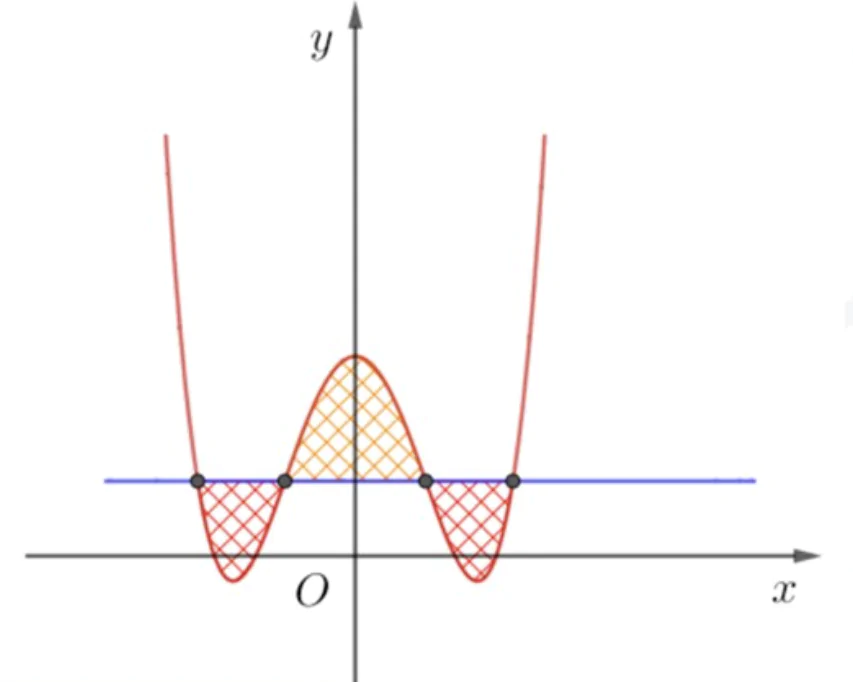
Chứng minh. Xét phương trình hoành độ giao điểm: 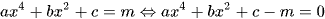 (1).
(1).
Đặt 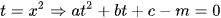 . Khi phương trình này có 2 nghiệm dương phân biệt
. Khi phương trình này có 2 nghiệm dương phân biệt 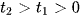 thì (1) có bốn nghiệm phân biệt là
thì (1) có bốn nghiệm phân biệt là 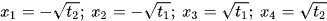 .
.
Quan sát đồ thị suy ra yêu cầu bài toán tương đương với: 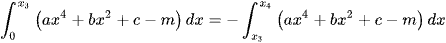 .
.
Biến đổi đưa về phương trình 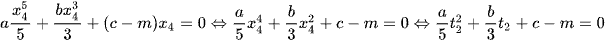 .
.
Mặt khác 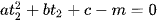 .
.
Suy ra 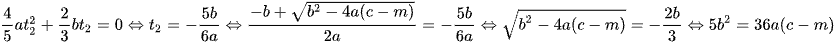 .
.