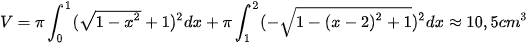Ứng dụng tích phân để giải một số bài toán thực tế | SBT Toán 12 - Cánh diều (SBT)

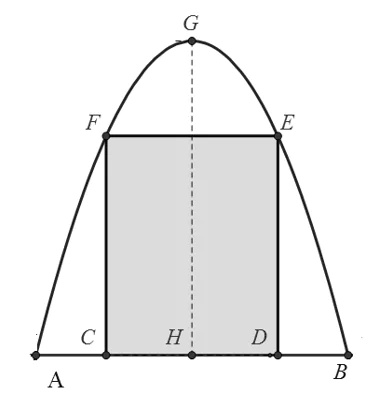
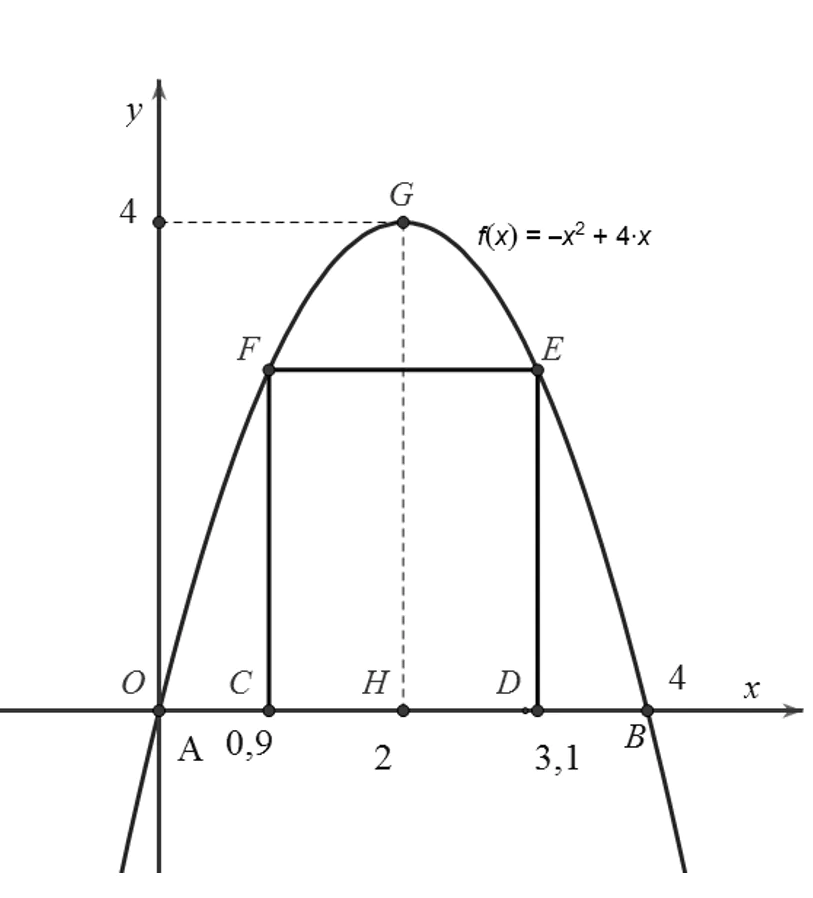
Câu 1: Một cái cổng hình Parabol như hình vẽ sau. Chiều cao GH=4m, chiều rộng AB=4m, AC=BD=0,9m. Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm có giá là 1200000 đồng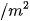, còn các phần để trắng làm xiên hoa có giá là 900000 đồng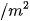. Hỏi tổng số tiền để làm hai phần nói trên là bao nhiêu?

Giải:

Gắn hệ trục tọa độ Oxy sao cho AB trùng Ox, A trùng O khi đó parabol có đỉnh G(2;4) và đi qua gốc tọa độ.

Giả sử phương trình của parabol có dạng .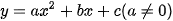

Vì parabol có đỉnh là G(2;4) và đi qua điểm O(0;0) nên ta có .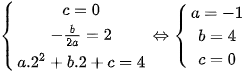

Suy ra phương trình parabol là .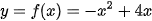

Diện tích của cả cổng là .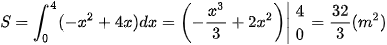

Mặt khác chiều cao CF=DE=f(0,9)-2,79(m); CD=4-2.0,9=2,2 (m) .

Diện tích hai cánh cổng là .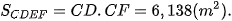

Diện tích phần xiên hoa là .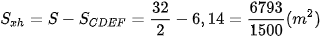

Vậy tổng số tiền để làm cổng là 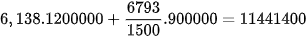đồng.

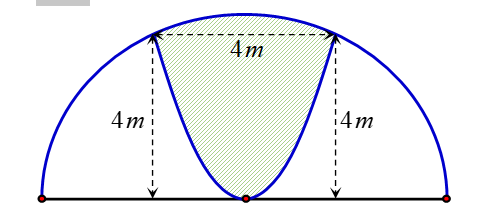
Câu 2: Một khuôn viên dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu) và cách nhau một khoảng bằng 4(m). Phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ, chi phí để trồng hoa và cỏ Nhật Bản tương ứng là 150.000 đồng/m² và 100.000 đồng/m². Hỏi cần bao nhiêu tiền để trồng hoa và trồng cỏ Nhật Bản trong khuôn viên đó? (Số tiền được làm tròn đến hàng đơn vị)

Giải:

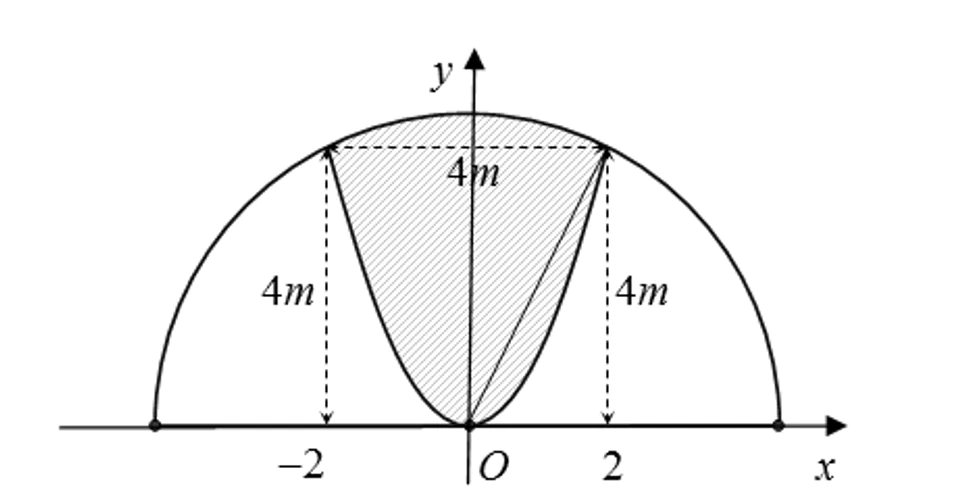
Chọn hệ trục Oxy như hình vẽ, ta có bán kính của đường tròn là .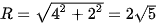

Phương trình của nửa đường tròn (C) là: .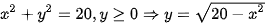

Parabol (P) có đỉnh O(0;0) và đi qua điểm (2;4) nên có phương trình: .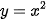

Diện tích phần tô màu là: .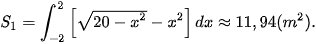

Diện tích phần không tô màu là: .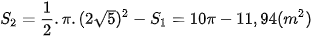

Số tiền để trồng hoa và trồng cỏ Nhật Bản trong khuôn viên đó là: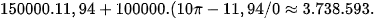

Câu 3: Một viên gạch hoa hình vuông cạnh . Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô mầu sẫm như hình vẽ bên). Diện tích mỗi cánh hoa của viên gạch bằng 

Giải:

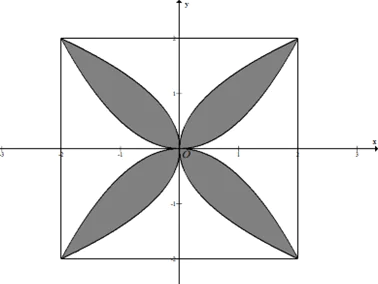
Chọn hệ tọa độ như hình vẽ (1 đơn vị trên trục bằng 10cm=1dm), các cánh hoa tạo bởi các đường parabol có phương trình .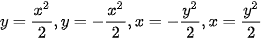

Diện tích một cánh hoa (nằm trong góc phàn tư thứ nhất) bằng diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 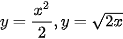và hai đường thẳng x=0; x=2.

Do đó diện tích một cánh hoa bằng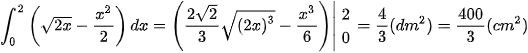

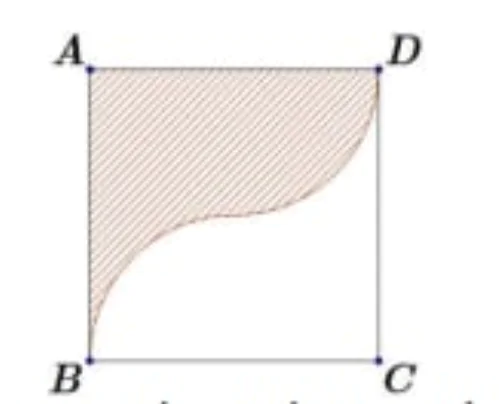
Câu 4: Một viên hồng ngọv có dạng một khối tròn xoay được tạo thành khi quay miền (H) (phần gạch chéo trong hình vẽ bên) quay quanh trục AD. Miền (H) được giới hạn bới cạnh AD của hình chữ nhật ABCD và các cung phần tư của các đường tròn tâm C, tâm I, (với I là trung điểm của cạnh AD), bán kính bằng 4. Tính thể tích của viên hồng ngọc đó.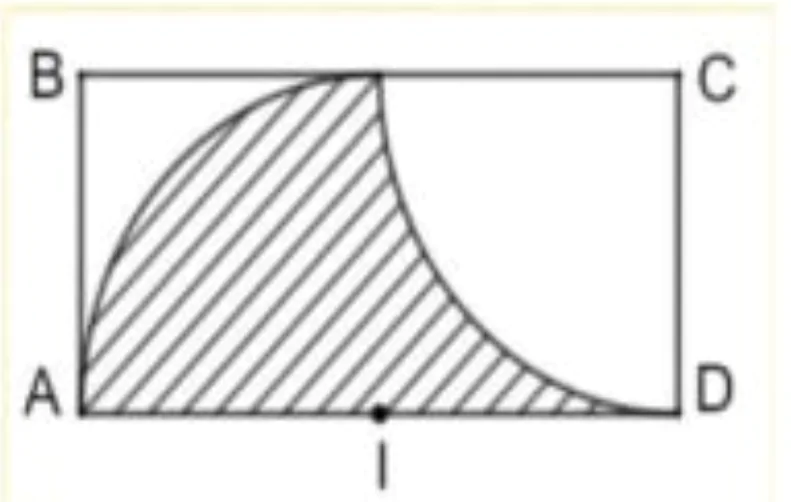

Giải 

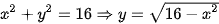
tâm I(0;0); R=4 có phương trình:

tâm C(4;4); R-4 có phương trình: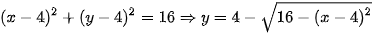

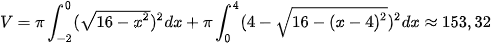
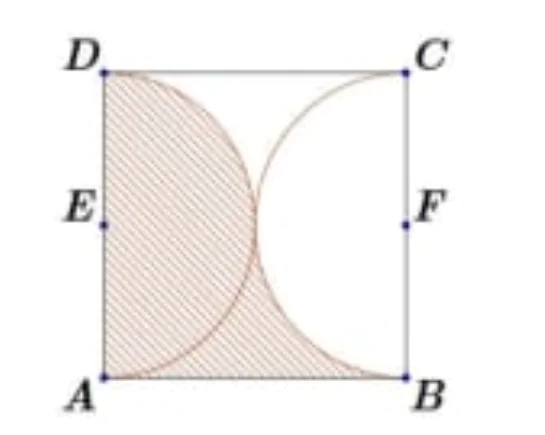
Câu 5: Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền(R) ( phần gạch chéo trong hình vẽ bên) quanh trục AB. Miền (R) được giới hạn bởi các cạnh AB, AD của hình vuông ABCD và các cung phần tư của các đường tròn bán kính bằng 1cm với tâm lần lượt là trung điểm của các cạnh BC, AD. Tính thể tích của vật trang trí đó.

Giải 

Chọn AB chứa trong trục Ox và .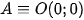

KHi đó E(0;1) và F(2;1) với E,F lần lượt là trung điểm của AD, BC.

Khi đó đường tròn tâm E chứa cung tròn AD là 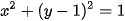và đường tròn tâm F chứa cung tròn BC là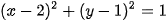

Suy ra phương trình cung trên của đường tròn tâm E là 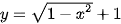và phương trình cung dưới của đường tròn tâm F là .

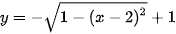Khi đó, thể tích vật thể trang trí là