Ứng dụng tích phân để giải bài toán chuyển động | SBT Toán 12 - Kết nối tri thức (SBT)
Ứng dụng tích phân để giải bài toán chuyển động
Dưới đây là công thức Ứng dụng tích phân để giải bài toán chuyển động
Ứng dụng tích phân để giải bài toán chuyển động
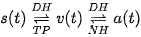
- Một vật chuyển động theo phương trình
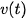 trong khoảng thời gian từ t=a đến t=b (a<b) sẽ di chuyển được quãng đường
trong khoảng thời gian từ t=a đến t=b (a<b) sẽ di chuyển được quãng đường 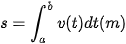 .
. - Quãng đường vật đi được trong giây thứ n là
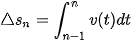 .
.
Ví Dụ
1. Một ô tô đang chạy với vận tốc là 12 (m/s) thì người lái đạp phanh; từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc v(t)=-6t+12 (m/s), trong đó t là khoảng thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến lúc ô tô dừng hẳn, ô tô còn di chuyển được bao nhiêu mét?
Giải:
Lấy mốc thời gian (t=0) là lúc đạp phanh.
Khi ô tô dừng hẳn thì vận tốc v(t)=0, tức là 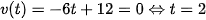
Vậy từ lúc đạp phanh đến lúc ô tô dừng hẳn, ô tô còn di chuyển được quãng đường là 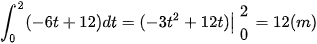 .
.
2. Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc 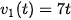 (m/s). Đi được 5s, người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốca=-70
(m/s). Đi được 5s, người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốca=-70 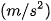 . Tính quãng đường đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
. Tính quãng đường đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
Giải:
Chọn gốc thời gian là lúc ô tô bắt đầu đi. Sau 5s ô tô đạt vận tốc là v(5)=35(m/s).
Sau khi phanh vận tốc ô tô là v(t)=35-70(t-5).
Ô tô dừng tại thời điểm t=5,5s.
Quãng đường ô tô đi được là 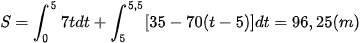 .
.
3. Để đảm bảo an toàn khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối thiểu 1m. Một ô tô A đang chạy với vận tốc 16m/s bỗng gặp ô tô B đang dừng đèn đỏ nên ô tô A hãm phanh và chuyển động chậm dần đều với vận tốc được biểu thị bởi công thức 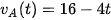 (đơn vị tính bằng ), thời gian tính bằng giây. Hỏi rằng để có 2 ô tô A và B đạt khoảng cách an toàn khi dừng lại thì ô tô A phải hãm phanh khi cách ô tô B một khoảng ít nhất là bao nhiêu?
(đơn vị tính bằng ), thời gian tính bằng giây. Hỏi rằng để có 2 ô tô A và B đạt khoảng cách an toàn khi dừng lại thì ô tô A phải hãm phanh khi cách ô tô B một khoảng ít nhất là bao nhiêu?
Giải:
Ta có: 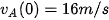 .
.
Khi xe A dừng hẳn: 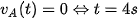 .
.
Quãng đường từ lúc xe A hãm phanh đến lúc dừng hẳn là 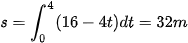 .
.
Do các xe phải cách nhau tối thiểu để đảm bảo an toàn nên khi dừng lại ô tô A phải hãm phanh khi cách ô tô B một khoảng ít nhất là 33m
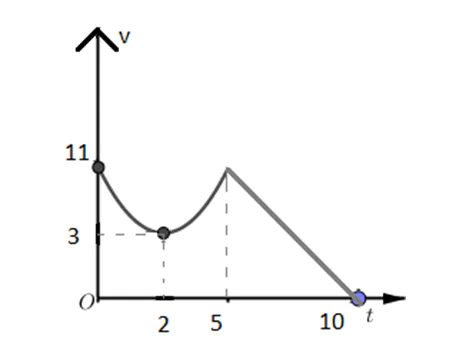
4. Chất điểm chuyển động theo quy luật vận tốc v(t) (m/s) có dạng đường Parapol khi 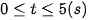 và v(t) có dạng đường thẳng khi
và v(t) có dạng đường thẳng khi 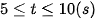 .Cho đỉnh Parapol là I(2,3). Hỏi quãng đường đi được chất điểm trong thời gian
.Cho đỉnh Parapol là I(2,3). Hỏi quãng đường đi được chất điểm trong thời gian 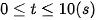 là bao nhiêu mét?
là bao nhiêu mét?
Giải:
Gọi Parapol 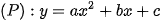 khi
khi 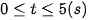
Do 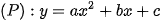 đi qua I(3;2); A(0;11) nên
đi qua I(3;2); A(0;11) nên 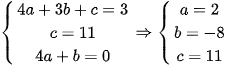
Khi đó quãng đường vật di chuyển trong khoảng thời gian từ 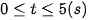 là
là 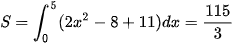
Ta có f(5)=21
Gọi d: y=ax+b khi 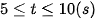 do d đi qua điểm B(5;21) và C(10;0) nên:
do d đi qua điểm B(5;21) và C(10;0) nên: 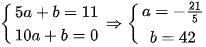
Khi đó quãng đường vật di chuyển trong khoảng thời gian từ 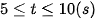 là
là 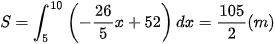
Quãng đường đi được chất điểm trong thời gian 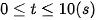 là
là 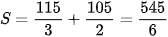 .
.
5. Một xe ô tô sau khi chờ hết đèn đỏ đã bắt đầu chuyển động với vận tốc được biểu thị bằng đồ thị là đường cong parabol như hình bên dưới. Biết rằng trong 5 phút thì xe đạt đến vận tốc cao nhất 1000 m/phút và bắt đầu giảm vận tốc, đi được 6 phút thì xe chuyển động đều
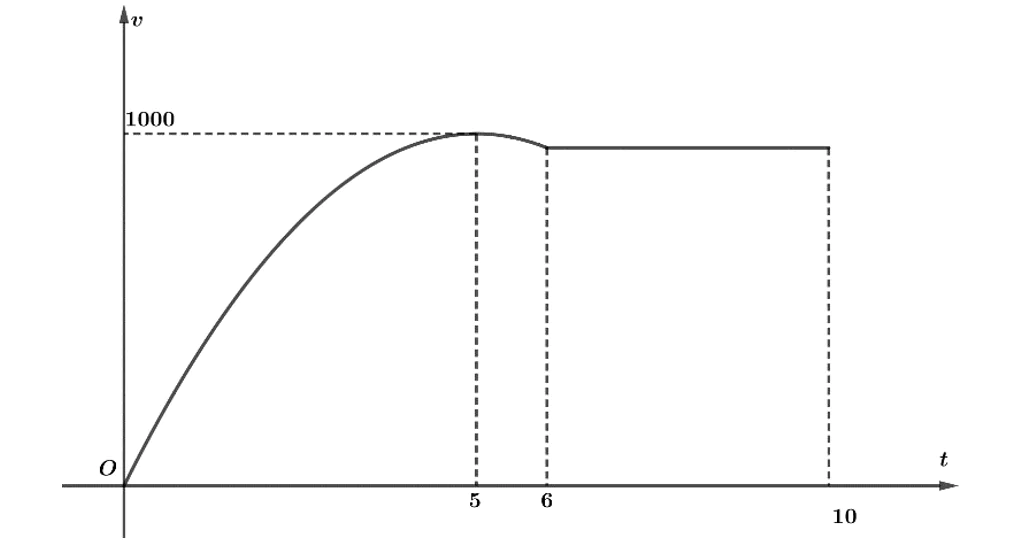
Hỏi quãng đường xe đã đi được trong 10 phút đầu tiên là bao nhiêu mét?
Giải:
Vận tốc ban đầu có dạng parabol nên có: 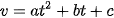 (m/phút).
(m/phút).
Ta có: 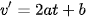 .
.
Dựa vào hình vẽ ta có: 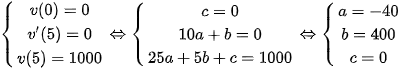 .
.
Vậy trong 6 phút đầu, ô tô đi với vận tốc có biểu thức 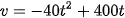 (m/phút).
(m/phút).
Khi 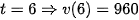 (m/phút).
(m/phút).
Như vậy từ phút thứ 6 đến phút thứ 10, ô tô chuyển động đều với vận tốc 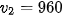 (m/phút)
(m/phút)
Quãng đường ô tô đi được trong 10 phút đầu là 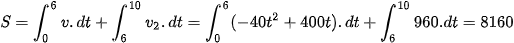 (m/phút).
(m/phút).