Ứng dụng phương pháp tọa độ giải bài toán hình học không gian | SGK Toán 12 - Chân trời sáng tạo
Ứng dụng phương pháp tọa độ giải bài toán hình học không gian
Dưới đây là công thức Ứng dụng phương pháp tọa độ giải bài toán hình học không gian
A. PHƯƠNG PHÁP GIẢI TOÁN
1. Phương pháp tổng quát: Để giải một bài toán hình học không gian tổng hợp bằng phương pháp tọa độ, ta thực hiện theo các bước sau:
Bước 1: Chọn hệ trục tọa Oxyz
Xác định ba đường thẳng đồng quy và đôi một cắt nhau trên cơ sở có sẵn của hình (như tam diện vuông, hình hộp chữ nhật, hình chóp tứ giác đều …), hoặc dựa trên các mặt phẳng vuông góc dựng thêm đường phụ.
Bước 2: Tọa độ hóa các điểm của hình không gian.
Tính tọa độ điểm liên quan trực tiếp đến giả thiết và kết luận của bài toán. Cơ sở tính toán chủ yếu dựa vào quan hệ song song, vuông góc cùng các dữ liệu của bài toán.
Bước 3: Chuyển giả thiết qua hình học giải tích.
Lập các phương trình đường, mặt liên quan. Xác định tọa độ các điểm, véc tơ cần thiết cho kết luận.
Bước 4: Giải quyết bài toán.
Sử dụng các kiến thức hình học giải tích để giải quyết yêu cầu của bài toán hình không gian.
Chú ý các công thức về góc, khoảng cách, diện tích và thể tích …
2. Cách chọn hệ tọa độ một số hình không gian
a. Hình hộp lập phương – Hình hộp chữ nhật ABCD.A'B'C'D'
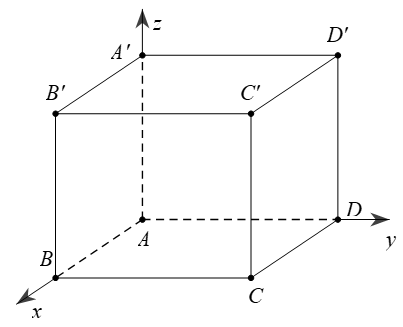
+ Với hình lập phương:
Chọn hệ trục tọa độ sao cho: 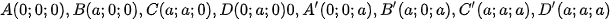
+ Với hình hộp chữ nhật:
Chọn hệ trục tọa độ sao cho: 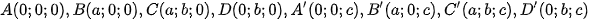
Chú ý: Tam diện vuông là một nửa của hình hộp chữ nhật nên ta chọn hệ trục tọa độ tương tự như hình hộp chữ nhật.
b. Với hình hộp đứng có đáy là hình thoi ABCD.A'B'C'D'
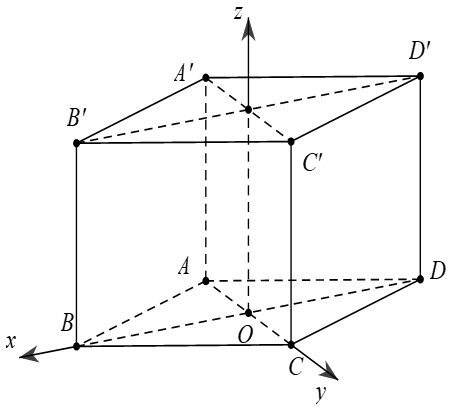
Chọn hệ trục tọa độ sao cho:
Gốc tọa độ trùng với giao điểm O của hai đường chéo của hình thoi ABCD
Trục Oz đi qua 2 tâm của 2 đáy.
Nếu 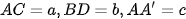 thì:
thì: 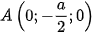 ,
, 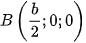 ,
, 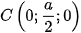 ,
,  ,
, 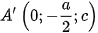 ,
, 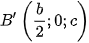 ,
, 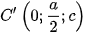 ,
, 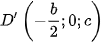
Chú ý: Với lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại B thì ta chọn hệ tọa độ tương tự như trên với gốc tọa độ là trung điểm AC,  ,
, 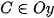 còn trục Oz đi qua trung điểm hai cạnh AC, A'C'
còn trục Oz đi qua trung điểm hai cạnh AC, A'C'
c. Hình chóp đều.
+ Hình chóp tam giác đều 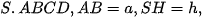 ta chọn hệ tọa độ sao cho O là trung điểm BC,
ta chọn hệ tọa độ sao cho O là trung điểm BC, 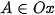 ,
, 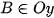
Khi đó 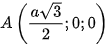 ,
, 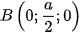 ,
, 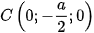 ,
, 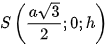 .
.
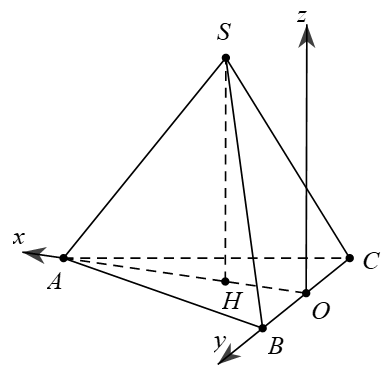
+ Hình chóp từ giác đều  , ta chọn hệ tọa độ sao cho O là tâm đáy
, ta chọn hệ tọa độ sao cho O là tâm đáy  ,
, 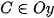 ,
, 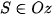 . Khi đó:
. Khi đó: 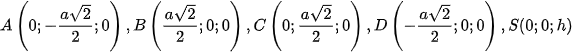
Chú ý: Ngoài cách chọn hệ trục như trên ta có thể chọn hệ trục bằng cách khác.
Chẳng hạn với hình chóp tam giác đều ta có thể chọn , trục Oy đi qua H và song song với BC
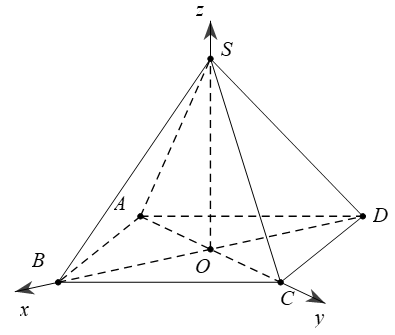
d. Hình chóp S.ABCD có ,
+ Nếu đáy là hình chữ nhật ta chọn hệ trục sao cho 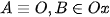 ,
, 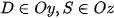
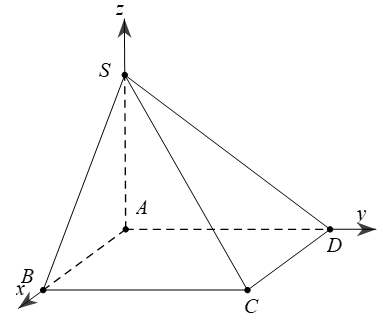
+ Nếu đáy là hình thoi, ta chọn hệ trục sao cho O là tâm của đáy, 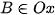 ,
, 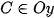 và
và 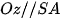
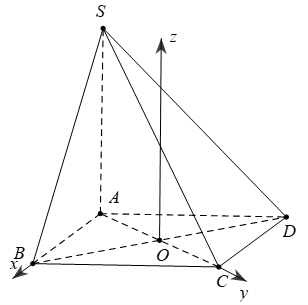
Chú ý: Cho hình chóp có
+ Nếu đáy ABC là tam giác vuông tại A thì cách chọn hệ trục hoàn toàn tương tự như hình chóp S.ABCD có đáy là hình chữ nhật.
+ Nếu đáy ABC là tam giác cân tại B thì ta chọn hệ trục tọa độ như hình chóp S.ABCD có đáy là hình thoi, khi đó gốc tọa độ là trung điểm cạnh AC.
e. Hình chóp S.ABCD có
Đường cao của tam giác là đường cao của hình chóp.
Nếu tam giác vuông tại , 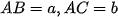 , ta chọn hệ trục sao cho
, ta chọn hệ trục sao cho  . Khi đó
. Khi đó 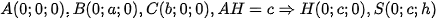
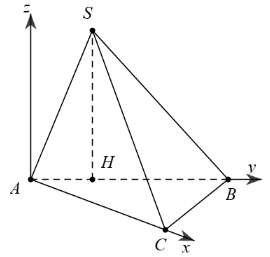
Chú ý:
+ Nếu vuông tại ta chọn , vuông tại chọn
+ Nếu tam giác cân tại , cân tại thì ta chọn 
Tùy vào từng bài toán mà có thể thay đổi linh hoạt cách chọn hệ tọa độ. Trong nhiều trường hợp, phải biết kết hợp kiến thức hình không gian tổng hợp và kiến thức hình giải tích nhằm thu gọn lời giải.
B. MỘT SỐ VÍ DỤ MINH HỌA
Ví dụ 1. Cho hình chóp có 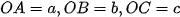 , đôi một vuông góc. Điểm cố định thuộc tam giác có khoảng cách lần lượt đến các mp(OBC), mp(OCA), mp(OAB) là 1, 2, 3. Tính a, b, c để thể tích O.ABC nhỏ nhất.
, đôi một vuông góc. Điểm cố định thuộc tam giác có khoảng cách lần lượt đến các mp(OBC), mp(OCA), mp(OAB) là 1, 2, 3. Tính a, b, c để thể tích O.ABC nhỏ nhất.
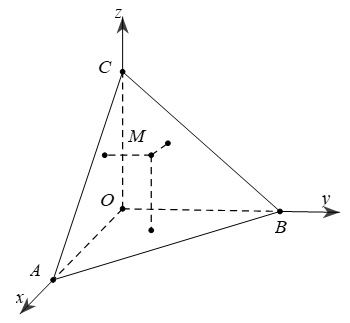
Chọn hệ trục tọa độ như hình vẽ, ta có: 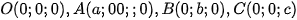
Vì khoảng cách từ M đến các mặt phẳng , , là 1, 2, 3 nên .
Suy ra phương trình  . Vì
. Vì 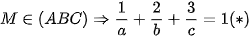 .
.
Thể tích khối chóp O.ABC:
Từ
Vậy đạt được khi 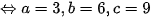
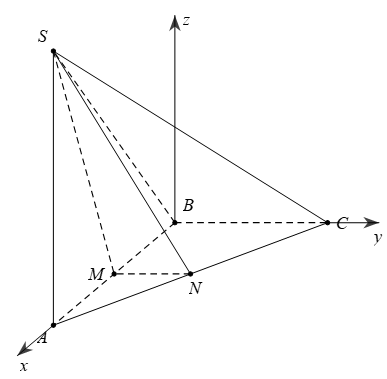
Ví dụ 2. Cho hình chóp S. có đáy ABCD là hình vuông cạnh 2a, , và mặt phẳng vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC. Tính theo a thể tích của khối chóp S.BMDN và tính cosin của góc giữa hai đường thẳng SM, DN.
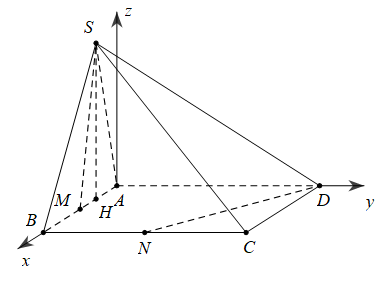
Gọi là hình chiếu của lên
Ta có: ,
Chọn hệ trục tọa độ như hình vẽ, ta có tọa độ các điểm: , , , , , , ,
Ta có
Thể tích khối chóp :
Vì ,
Vậy 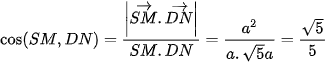 .
.
Ví dụ 4. Trong không gian , cho hình hộp chữ nhật có , , , và , ,
1. Tìm tọa độ các đỉnh của hình hộp.
2. Tìm điểm E trên đường thẳng sao cho
3. Tìm điểm M thuộc , thuộc sao cho , . Từ đó tính khoảng cách giữa hai đường thẳng chéo nhau A'C và BD.

1. Ta có 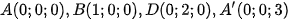
Hình chiếu của lên là , hình chiếu của lên là nên
Hình chiếu của , , lên mp và trục lần lượt là các điểm 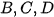 và nên
và nên 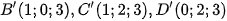
2. Vì thuộc đường thẳng nên , suy ra
Mà nên Vậy .
3. Đặt ;
Ta có:
, suy ra
Theo giả thiết của để bài, ta có:
Mà , ,
Khi đó trở thành: 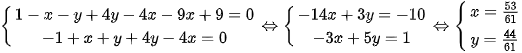
Do đó ,
Vì là đường vuông góc chung của hai đường thẳng ,
Ví dụ 5. Cho hình chóp có đáy là tam giác vuông cân tại , ; hai mặt phẳng và cùng vuông góc với mặt phẳng Gọi là trung điểm của ; mặt phẳng và song song với , cắt tại Biết góc giữa hai mặt phẳng và bẳng Tính thể tích khối chóp và khoảng cách giữa hai đường thẳng AB và SN theo a
Vì hai mặt phẳng và cùng vuông góc với mặt phẳng 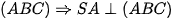
Chọn hệ trục tọa độ như hình vẽ, đặt ,
Vì 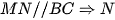 là trung điểm
là trung điểm
Tọa độ các đỉnh là: , , , , ,
Suy ra  .
.
Do đó:
là VTPT của mặt phẳng
là VTPT của mặt phẳng 
Theo giả thiết ta có: 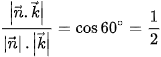
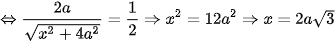 .
.
Vì  là trung điểm của
là trung điểm của 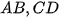 nên:
nên: 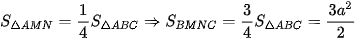
Từ đó suy ra thể tích khối chóp là:
Ta có: 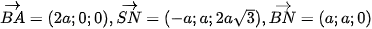 .
.
Suy ra 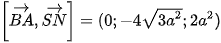
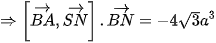 .
.
Vậy 