Nguyên hàm và tích phân của hàm phân thức hữu tỉ

Đó là nguyên hàm 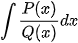hoặc tích phân  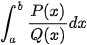 với 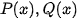là các đa thức.

Trường hợp đơn giản nhất của dạng toán này là nguyên hàm 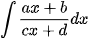 ta phân tích tử theo mẫu như sau:

Ví dụ 1: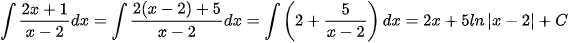

Ví dụ 2: Có bao nhiêu số thực dương a để ?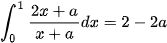

Giải. Ta có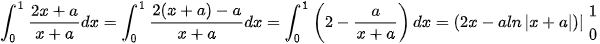

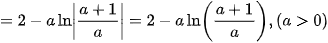
Vậy .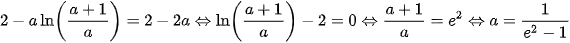

Áp dụng phương pháp tương tự như vậy cho các nguyên hàm dạng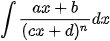

Ví dụ 4: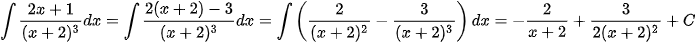 

Ví dụ 5: Có bao nhiêu số thực dương $a$ đ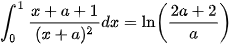ể ?

Giải. Ta có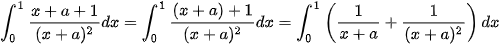

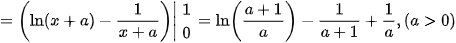
Vậy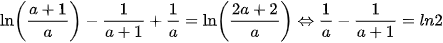

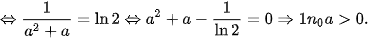
Phương pháp chung để tìm nguyên hàm và tính tích phân của hàm phân thức hữu tỉ: ta căn cứ vào bậc của tử và mẫu; cùng dạng của mẫu

*Bậc của tử lớn hơn hoặc bằng bậc của mẫu trước tiên dùng phép chia đa thức P(x) chia cho Q(x) ta được P(x)=T(x)Q(x)+R(x) hay .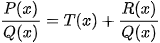

Nếu chia đa thức bằng MTCT các em thực hiện như sau:

Bước 1: Nhập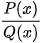 và CALC với $x=1000$

Bước 2: Lấy phần nguyên của kết quả đó chính là thương T(x)

Bước 3: Phần dư suy từ đẳng thức 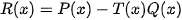 và CALC với $x=1000$

Cách 2: Với MTCT hỗ trợ phép chia có dư (chẳng hạn 580) các em thực hiện nhanh như sau:

Bước 1: Nhập 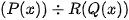và CALC với $x=1000$

Bước 2: Kết quả $T\left(x\right),R=R(x)\; ($phân tích ngược lại như cách trên)

*Để nhập $÷R$ các em nhấn ALPHA và dấu phân số; trong cả hai cách trên các em có thể CALC với $x=100.$

Ví dụ 1: Thực hiện phép chia đa thức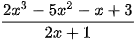

Bước 1: Nhập 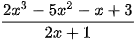và CALC với $x=1000$

Bước 2: Phần nguyên của kết quả là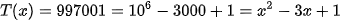

Bước 3: Phần dư là 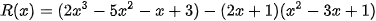 và CALC với $x=1000$ cho kết quả R(x)=2

Vậy .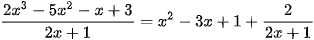

Ví dụ 2: Thực hiện phép chia đa thức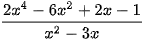

Bước 1: Nhập 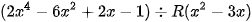 và CALC với $x=100$

Bước 2: Kết qu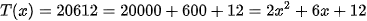ả và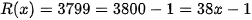

Vậy .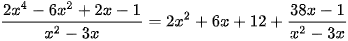

*Bậc của tử nhỏ hơn bậc của mẫu, thực hiện theo 3 khả năng sau:

Dạng 1: 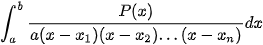phân tích .

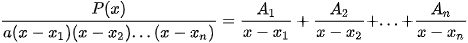Dạng 2: 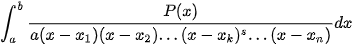phân tích .

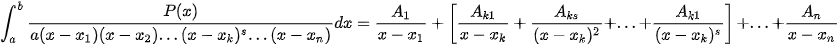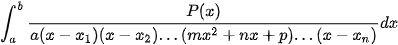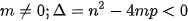Dạng 3: với  phân tích .

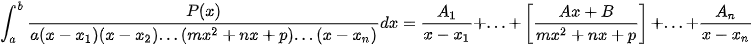Các hệ số trong các phân tích trên tìm ra bằng cách quy đồng rút gọn sau đó đồng nhất hệ số của $x^n$ hai vế hoặc chọn các giá trị của $x$ đưa về giải hệ phương trình hoặc sử dụng MTCT.

ĐẶC BIỆT: ;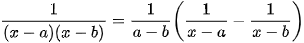

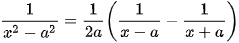
Xác định các hệ số trong phân tích bằng MTCT

Dạng 1: 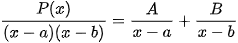 các hệ số A,B xác định nhanh bằng MTCT như sau: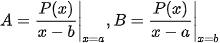

Dạng 2: 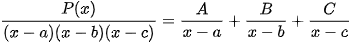các hệ số A,B,C xác định nhanh bằng MTCT như sau: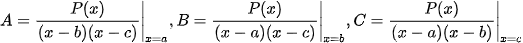

Dạng 3: 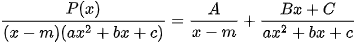các hệ số A,B,C xác định nhanh bằng MTCT như sau: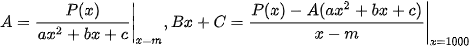

Dạng 4: 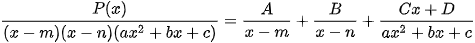các hệ số A,B,C,D xác định nhanh bằng MTCT như sau:

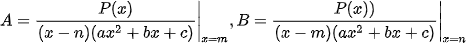và .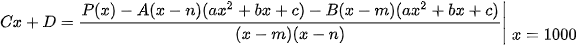

Các nguyên hàm phân thức hữu tỉ cần ghi nhớ để áp dụng

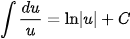
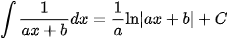
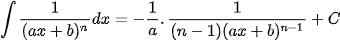
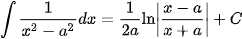
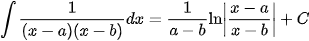
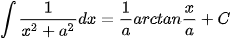
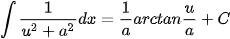
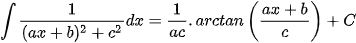
Các ví dụ phải sử dụng phép chia đa thức trước (bậc tử lớn hơn hoặc bằng bậc mẫu)

Ví dụ 1: Tìm nguyên hàm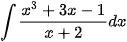 

Giải. Dùng phép chia đa thức ta có

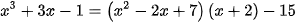
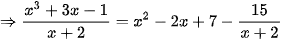
Ví dụ 2: Tìm nguyên hàm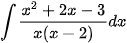

Giải. Thực hiện phép chia đa thức ta có thương và dư là 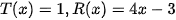 kết hợp với phân tích ta có:

.

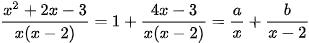
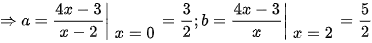
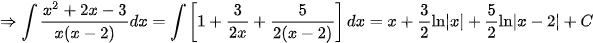Đối với nguyên hàm dạng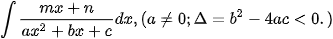

Bước 1: Phân tích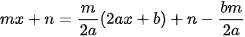

Bước 2: Khi đó 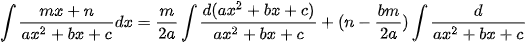 và áp dụng các nguyên hàm phía trên.

Ví dụ 2: Biết rằng 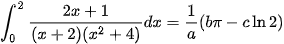với a,b,c là các số nguyên dương và 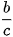là phân số tối giản. Giá trị của a+b+c bằng

Giải. Phân tích:

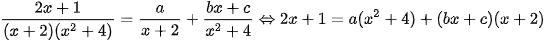
Cho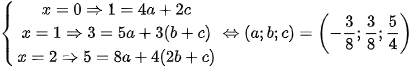

Vậy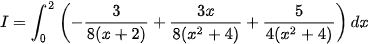

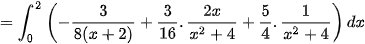
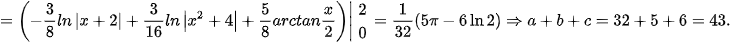
Các trường hợp đặc biệt của nguyên hàm – tích phân hàm phân thức hữu tỉ

Dạng 1: 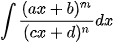 với m,n là các số nguyên dương lớn

Phương pháp chung là đổi biến 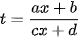cùng quan sát các ví dụ sau:

Ví dụ 1: Cho 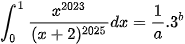với $a,b$ là các số nguyên, $a$ và $3$ là hai số nguyên tố cùng nhau. Giá trị a+b bằng

Giải. Ta có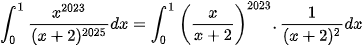

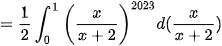
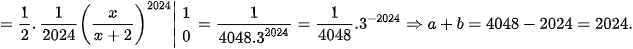
Một số bài toán có luỹ thừa bậc cao của hàm phân thức hữu tỉ, ta chú ý các phép đổi biến hoặc đưa về biểu thức vi phân hay thực hiện phép chia cho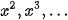

Ví dụ 1: Biết 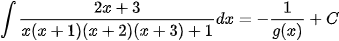. Tổng các nghiệm của phương trình g(x)=0  là

Giải.

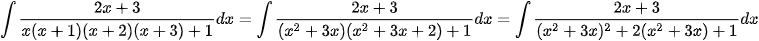
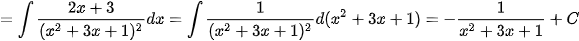
Vậy 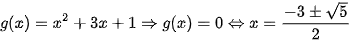.