Bất đẳng thức với hai căn thức cơ bản | SBT Toán 12 - Cánh diều (SBT)
Bất đẳng thức với hai căn thức cơ bản
Dưới đây là công thức Bất đẳng thức với hai căn thức cơ bản
Các bất đẳng thức cơ bản cần nhớ áp dụng trong các bài toán giá trị lớn nhất và giá trị nhỏ nhất
Bất đẳng thức với hai căn thức cơ bản
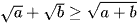. Dấu bằng xảy ra khi và chỉ khi a = 0 hoặc b = 0.
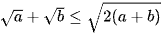. Dấu bằng xảy ra khi và chỉ khi a = b.
Ví dụ 1: Cho hai số thực x, y thoả mãn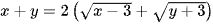 
. Tìm giá trị nhỏ nhất của biểu thức 
.
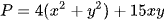A. minP = -80.
B. minP = -91.
C. minP = -83.
D. minP = -63.
Lời giải
Ta có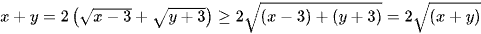 
. Suy ra x + y = 0 hoặc x + y ≥ 4.
Và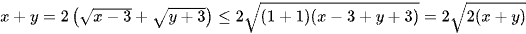 
⇒ x + y ≤ 8.
Nếu x + y = 0 ⇔ x = 3; y = -3 ⇒ P = -63.
Nếu x + y ∈ [4; 8], xuất phát từ điều kiện xác định căn thức ta có: (x - 3)(y + 3) ≥ 0 ⇒ xy ≥ 3(y - x) + 9.
Suy ra
.
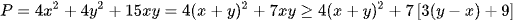
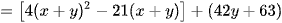
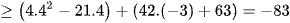Dấu bằng đạt tại x = 7; y = -3. Đối chiếu hai trường hợp ta Chọn đáp án C.
*Chú ý: Hàm số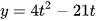 
đồng biến trên đoạn [4; 8] nên ta có đánh giá 
.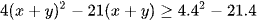