Bất đẳng thức AM – GM (Sách giáo khoa việt nam gọi là bất đẳng thức Côsi) | SBT Toán 12 - Cánh diều (SBT)

Các bất đẳng thức cơ bản cần nhớ áp dụng trong các bài toán giá trị lớn nhất và giá trị nhỏ nhất

Bất đẳng thức AM – GM (Sách giáo khoa việt nam gọi là bất đẳng thức Côsi)

Với hai số thực không âm ta có 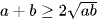. Dấu bằng xảy ra khi và chỉ khi a = b.

Với ba số thực không âm ta có 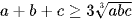. Dấu bằng xảy ra khi và chỉ khi a = b = c.

Với n thực không âm ta có 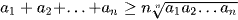. Dấu bằng xảy ra khi và chỉ khi .

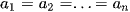Ví dụ 1: Cho a > 0, b > 0 thoả mãn 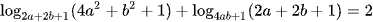. Giá trị biểu thức a + 2b bằng

A. .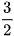

B. 5.

C. 4.

D. .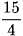

Lời giải 

Chú 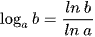ý . Vậy .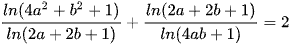

Sử dụng AM – GM có

.

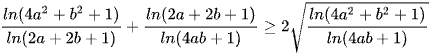Mặt khác .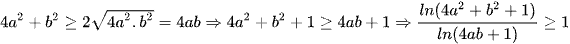

Do đó dấu bằng phải xảy ra tức  .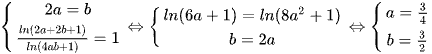

Do đó a + 2b = .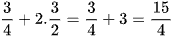

Chọn đáp án D.

Ví dụ 2: Cho các số thực dương x, y, z. Biết giá trị nhỏ nhất của biểu thức 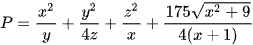 là 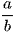với a, b là các số nguyên dương và 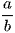tối giản. Tính S = a + b.

A. S = 52.

B. S = 207.

C. S = 103.

D. S = 205.

Lời giải

Ta đánh giá ba số hạng đầu để mất biến y và z bằng cách sử dụng bất đẳng thức AM – GM ta có

.

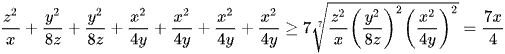Vậy P ≥ f(x) = .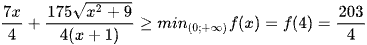

Chọn đáp án B.

Dấu bằng đạt tại 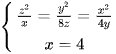⇔ (x; y; z) = (4; 4; 2).

Ví dụ 3: Cho các số thực a, b, c lớn hơn 1 thoả mãn 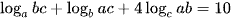. Tính giá trị biểu thức P = .

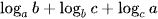A. P = 5.

B. .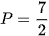 

C. .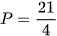

D. .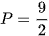

Lời giải

Chú ý biến đổi logarit 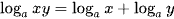(x > 0; y > 0), 0 < a ≠ 1.

Vậy đẳng thức giả thiết tương đương với: 

.

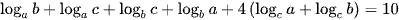
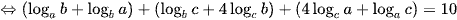Do a, b, c lớn hơn 1 nên 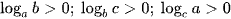và để ý tính chất 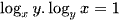(0 < x, y ≠ 1).

Sử dụng bất đẳng thức AM – GM ta có:

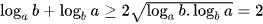
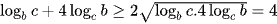
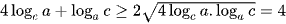
Cộng lại theo vế ta có: .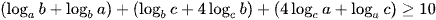

Điều đó chứng tỏ phải xảy ra dấu bằng  trong các bất đẳng thức AM – GM

Dấu bằng đạt tại .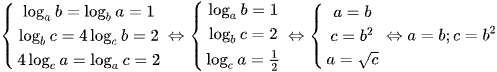

Chọn đáp án B.

Ví dụ 4: Có tất cả bao nhiêu bộ ba số thực (x; y; z) thoả mãn đồng thời các điều kiện dưới đây 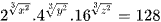 và .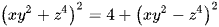

A. 8.

B. 4.

C. 3.

D. 2.

Lời giải

Ta có .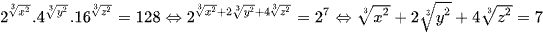

Khai thác điều kiện số 2, ta có

.

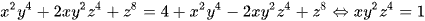Mặt khác theo bất đẳng thức AM – GM cho 7 số thực dương ta có

.

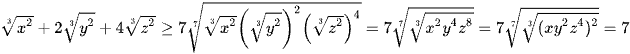Do đó dấu bằng phải xảy ra tức 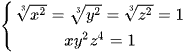⇔ x = 1; y, z ∈ {-1; 1}.

Mỗi số y, z có 2 cách vậy có tất cả 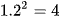bộ số thực thoả mãn.

Chọn đáp án B.