Bất đẳng thức Cauchy – Schwarz (Sách giáo khoa Việt Nam gọi là bất đẳng thức Bunhiacopsky) | SBT Toán 12 - Cánh diều (SBT)
Bất đẳng thức Cauchy – Schwarz (Sách giáo khoa Việt Nam gọi là bất đẳng thức Bunhiacopsky)
Dưới đây là công thức Bất đẳng thức Cauchy – Schwarz (Sách giáo khoa Việt Nam gọi là bất đẳng thức Bunhiacopsky)
Các bất đẳng thức cơ bản cần nhớ áp dụng trong các bài toán giá trị lớn nhất và giá trị nhỏ nhất
Bất đẳng thức Cauchy – Schwarz (Sách giáo khoa Việt Nam gọi là bất đẳng thức Bunhiacopsky)
Ta luôn có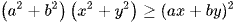 
. Dấu bằng xảy ra khi và chỉ khi 
.
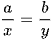Ta hay sử dụng: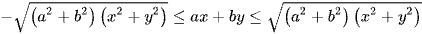 
.
Dấu bằng bên phải đạt tại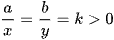 
; dấu bằng bên trái đạt tại 
.
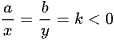Ta luôn có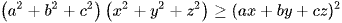 
. Dấu bằng xảy ra khi và chỉ khi 
.
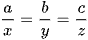Ta luôn có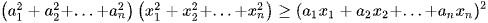 
. Dấu bằng xảy ra khi và chỉ khi 
.
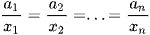Ví dụ 1: Cho hai số thực x, y thoả mãn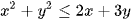 
. Giá trị lớn nhất của biểu thức 2x + y bằng
A.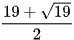 
.
B.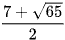 
.
C.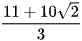 
.
D.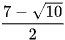 
.
Lời giải
Ta có biến đổi giả thiết: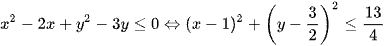 
.
Khi đó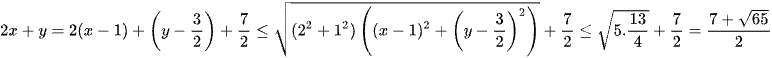 
.
Dấu bằng đạt tại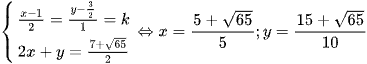 
.
Chọn đáp án B.
Ví dụ 2: Cho các số thực x, y, z thoả mãn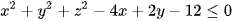 
. Giá trị lớn nhất của biểu thức 2x + 3y - 2z bằng
A. 17.
B. 25.
C. 21.
D. 24.
Lời giải
Biến đổi giả thiết có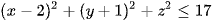 
.
Khi đó
2x + 3y - 2z = (2(x - 1) + 3(y + 1) - 2z) + 4
.
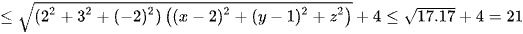Dấu bằng đạt tại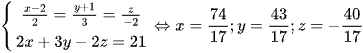 
.
Chọn đáp án C.
Ví dụ 3: Cho hai số thực x, y thay đổi thoả mãn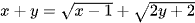 
. Gọi a, b lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 
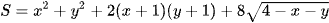. Tính P = a + b.
A. P = 44.
B. P = 41.
C. P = 43.
D. P = 42.
Lời giải
Ta có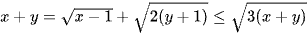 
⇒ t = x + y ∈ [0; 3].
Khi đó
.
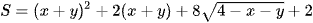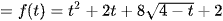∈ [18; 25], ∀t ∈ [0; 3] ⇒ P = 18 + 25 = 43.
Chọn đáp án C.
Ví dụ 4: Số phức z thoả mãn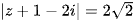 
, giá trị lớn nhất của biểu thức 
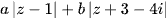, (a, b > 0) bằng
Lời giải
Đặt z = x + yi ⇒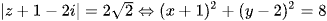 
.
Khi đó sử dụng bất đẳng thức Cauchy – Schwarz có
.
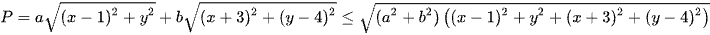
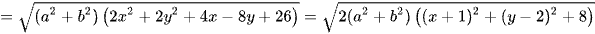
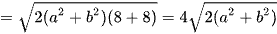Chọn đáp án B.