Bất đẳng thức Mincopski (bất đẳng thức véctơ) | SBT Toán 12 - Cánh diều (SBT)
Bất đẳng thức Mincopski (bất đẳng thức véctơ)
Dưới đây là công thức Bất đẳng thức Mincopski (bất đẳng thức véctơ)
Các bất đẳng thức cơ bản cần nhớ áp dụng trong các bài toán giá trị lớn nhất và giá trị nhỏ nhất
Bất đẳng thức Mincopski (bất đẳng thức véctơ)
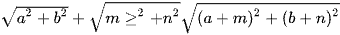. Dấu bằng xảy ra khi và chỉ khi 
.
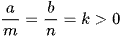Ví dụ 1: Giá trị nhỏ nhất của biểu thức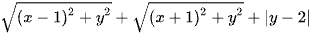 
bằng
A.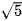 
.
B. 2.
C.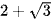 
.
D.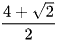 
.
Lời giải
Sử dụng bất đẳng thức Mincopsky ta có
.
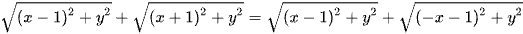
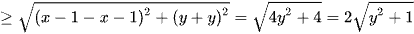Do đó
.
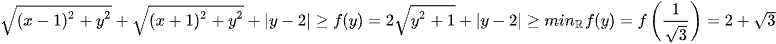Dấu bằng đạt tại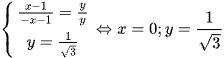 
.
Chọn đáp án C.
Ví dụ 2: Cho hai số thực a, b thoả mãn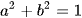 
. Biểu thức 
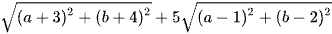có giá trị nhỏ nhất bằng
A.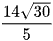 
.
B.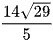 
.
C. 15.
D.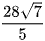 
.
Lời giải
Ta biến đổi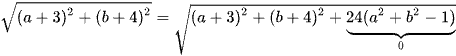 
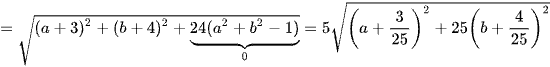
Vậy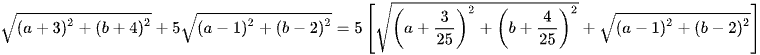 
.
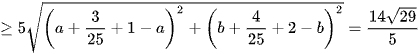Dấu bằng đạt tại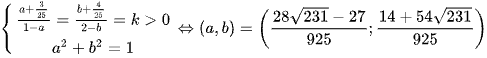 
.
Chọn đáp án B.
Câu 32: Trong không gian Oxyz, cho mặt cầu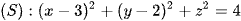 
và hai điểm A(-1; 2; 0), B(2; 5; 0). Điểm M(a; b; c) thuộc (S) sao cho MA + 2MB đạt giá trị nhỏ nhất, giá trị của a - b + c bằng
A.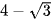 
.
B.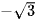 
.
C.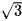 
.
D.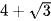 
.
Lời giải
Có M ∈ (S) ⇒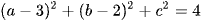 
. Khi đó sử dụng bất đẳng thức Mincopski có
MA + 2MB =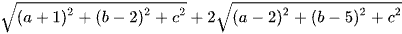 
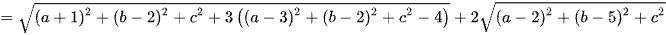
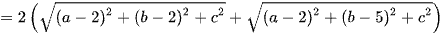
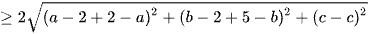= 6.
Dấu bằng đạt tại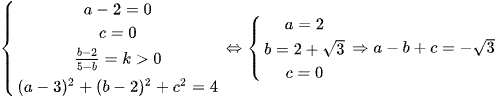 
.
Chọn đáp án B.
Câu 33: Trong không gian Oxyz, cho mặt cầu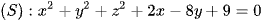 
và hai điểm A(5; 10; 0), B(4; 2; 1). Xét điểm M di động trên (S), giá trị nhỏ nhất của biểu thức MA + 3MB bằng
A.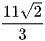 
.
B.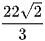 
.
C.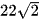 
.
D.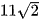 
.
Lời giải
Gọi M(x; y; z) ∈ (S) ⇒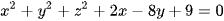 
. Khi đó sử dụng bất đẳng thức Mincopski có
MA + 3MB =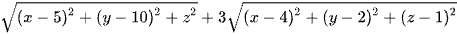 
.
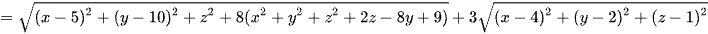
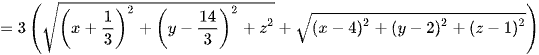
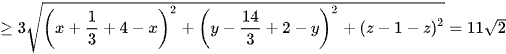Dấu bằng đạt tại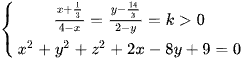 
.
Chọn đáp án D.