Số gần đúng và sai số. Cách quy tròn số gần đúng | Toán 10 - Cánh diều
Số gần đúng và sai số. Cách quy tròn số gần đúng. Toán 10 chương 6 Thống kê.
Dưới đây là công thức Số gần đúng và sai số. Cách quy tròn số gần đúng
1. Số gần đúng Trong nhiều trường hợp ta không thể biết hoặc khó biết số đúng (kí hiệu 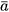 ) mà ta chỉ tìm được giá trị khá xấp xỉ nó. Giá trị này được gọi là số gần đúng kí hiệu là a.
) mà ta chỉ tìm được giá trị khá xấp xỉ nó. Giá trị này được gọi là số gần đúng kí hiệu là a.
Ví dụ: giá trị gần đúng của 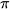 là 3,14 hay 3,14159 ; còn đối với
là 3,14 hay 3,14159 ; còn đối với 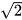 là 1,41 hay 1,414 ; Như vậy có sự sai lệch giữa giá trị chính xác của một đại lượng và giá trị gần đúng của nó. Để đánh giá mức độ sai lệch đó, người ta đưa ra khái niệm sai số tuyệt đối.
là 1,41 hay 1,414 ; Như vậy có sự sai lệch giữa giá trị chính xác của một đại lượng và giá trị gần đúng của nó. Để đánh giá mức độ sai lệch đó, người ta đưa ra khái niệm sai số tuyệt đối.
2. Sai số tuyệt đối và sai số tương đối
a) Sai số tuyệt đối của số gần đúng
Giá trị 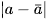 phản ánh mức độ sai lệch giữa số đúng
phản ánh mức độ sai lệch giữa số đúng 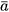 và số gần đúng a, được gọi là sai số tuyệt đối của số gần đúng a, kí hiệu là
và số gần đúng a, được gọi là sai số tuyệt đối của số gần đúng a, kí hiệu là 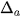 , tức là:
, tức là: 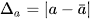 .
.
Độ chính xác của một số gần đúng
Trong thực tế, nhiều khi ta không biết 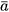 nên ta không tính được
nên ta không tính được 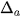 . Tuy nhiên ta có thể đánh giá
. Tuy nhiên ta có thể đánh giá 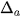 không vượt quá một số dương d nào đó.
không vượt quá một số dương d nào đó.
Nếu 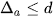 thì
thì 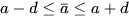 , khi đó ta viết
, khi đó ta viết 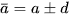
d gọi là độ chính xác của số gần đúng.
b) Sai số tương đối
Sai số tương đối của số gần đúng a, kí hiệu là 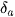 là tỉ số giữa sai số tuyệt đối và
là tỉ số giữa sai số tuyệt đối và 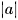 , tức là
, tức là 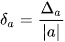 .
.
Nhận xét: Nếu 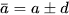 thì
thì 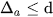 suy ra
suy ra 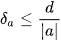 . Do đó
. Do đó 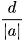 càng nhỏ thì chất lượng của phép đo đặc hay tính toán càng cao.
càng nhỏ thì chất lượng của phép đo đặc hay tính toán càng cao.
3. Quy tròn số gần đúng
Số thu được sau khi thực hiện làm tròn số được gọi là số quy tròn. Số quy tròn là một số gần đúng của số ban đầu.
Quy tắc quy tròn các số như sau:
Nếu chữ số ngay sau hàng quy tròn nhỏ hơn 5 thì ta chỉ việc thay chữ số đó và các chữ số bên phải nó bởi 0 .
Nếu chữ số ngay sau hàng quy tròn lớn hơn hay bằng 5 thì ta thay chữ số đó và các chữ số bên phải nó bởi 0 và cộng thêm một đơn vị vào số hàng làm tròn.
Nhận xét: Khi thay số đúng bởi số qui tròn đến một hàng số nào đó thì sai số tuyệt đối của số qui tròn không vượt quá nửa đơn vị của hàng qui tròn.
Như vậy, độ chính xác của số qui tròn bằng nửa đơn vị của hàng qui tròn.
Chú ý: Các viết số quy tròn của số gần đúng căn cứ vào độ chính xác cho trước.
Cho số gần đúng a với độ chính xác d. Khi được yêu cầu quy tròn a mà không nói rõ quy tròn đến hàng nào thì ta quy tròn a đến hàng cao nhất mà d nhỏ hơn một đơn vị của hàng đó.
Xác định số quy tròn của số gần đúng với độ chính xác cho trước:
Các bước xác định số quy tròn của số gần đúng a với độ chính xác d cho trước:
Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của d .
Bước 2: Quy tròn số a ở hàng gấp 10 lần hàng tìm được ở Bước 1 .
Xác định số gần đúng của một số với độ chính xác cho trước:
Để tìm số gần đúng a của số đúng 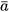 với độ chính xác d , ta thực hiện các bước sau:
với độ chính xác d , ta thực hiện các bước sau:
Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của d.
Bước 2: Quy tròn 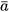 đến hàng tìm được ở trên.
đến hàng tìm được ở trên.
4. Chữ số chắc (đáng tin)
Cho số gần đúng a của số 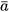 với độ chính xác d. Trong số a một chữ số được gọi là chữ số chắc (hay đáng tin) nếu d không vượt quá nửa đơn vị của hàng có chữ số đó.
với độ chính xác d. Trong số a một chữ số được gọi là chữ số chắc (hay đáng tin) nếu d không vượt quá nửa đơn vị của hàng có chữ số đó.
Nhận xét: Tất cả cá chữ số đứng bên trái chữ số chắc đều là chữ số chắc. Tất cả các chữ số đứng bên phải chữ số không chắc đều là chữ số không chắc.
5. Dạng chuẩn của số gần đúng
Nếu số gần đúng là số thập phân không nguyên thì dạng chuẩn là dạng mà mọi chữ số của nó đều là chữ số chắc chắn.
Nếu số gần đúng là số nguyên thì dạng chuẩn của nó là:  trong đó A là số nguyên, k là hàng thấp nhất có chữ số chắc
trong đó A là số nguyên, k là hàng thấp nhất có chữ số chắc 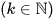 . (suy ra mọi chữ số của A đều là chữ số chắc chắn).
. (suy ra mọi chữ số của A đều là chữ số chắc chắn).
Khi đó độ chính xác 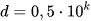 .
.
6. Kí hiệu khoa học của một số
Mọi số thập phân khác 0 dều viết được dưới dạng 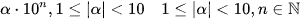 (Quy ước
(Quy ước 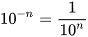 ) dạng như vậy được gọi là kí hiệu khoa học của số đó.
) dạng như vậy được gọi là kí hiệu khoa học của số đó.
Một số bài tập ứng dụng công thức Số gần đúng và sai số. Cách quy tròn số gần đúng:
Bài 5.1 trang 77 Toán 10 Tập 1
Bài 5.1 trang 77 Toán 10 Tập 1: Trong các số sau, những số nào sau đây là số gần đúng?
a) Cân một túi gạo cho kết quả là 10,2 kg.
b) Bán kính Trái Đất là 6 371 km.
c) Trái Đất quay một vòng quanh Mặt Trời mất 365 ngày.
Bài 5.2 trang 77 Toán 10 Tập 1
Bài 5.2 trang 77 Toán 10 Tập 1: Giải thích kết quả: “Đo độ cao của một ngọn núi cho kết quả là 1235 ± 5m” và thực hiện làm tròn số gần đúng.
Bài 5.3 trang 77 Toán 10 Tập 1
Bài 5.3 trang 77 Toán 10 Tập 1: Sử dụng máy tính cầm tay tìm số gần đúng cho 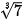 với độ chính xác 0,0005.
với độ chính xác 0,0005.
Bài 5.4 trang 77 Toán 10 Tập 1
Bài 5.4 trang 77 Toán 10 Tập 1: Các nhà Vật lí sử dụng ba phương pháp đo hằng số Hubble lần lượt cho kết quả như sau:
67,31 ± 0,96;
67,9 ± 0,55;
67,74 ± 0,46;
Phương pháp nào chính xác nhất tính theo sai số tương đối?
Bài 5.5 trang 77 Toán 10 Tập 1
Bài 5.5 trang 77 Toán 10 Tập 1: An và Bình cùng tính chu vi của hình tròn bán kính 2 cm với hai kết quả như sau:
Kết quả của An: S1 = 2πR = 2.3,14.2 = 12,56.
Kết quả của Bình: S2 = 2πR = 2.3,1.2 = 12,4.
Hỏi:
a) Hai giá trị tính được có phải là các số gần đúng không?
b) Giá trị nào chính xác hơn?
Bài 5.6 trang 77 Toán 10 Tập 1
Bài 5.6 trang 77 Toán 10 Tập 1: Làm tròn số 8316,4 đến hàng chục và 9,754 đến hàng phần trăm rồi tính sai số tuyệt đối của số quy tròn.
Bài 1 trang 109 Toán lớp 10 Tập 1
Bài 1 trang 109 Toán lớp 10 Tập 1: Ở Babylon, một tấm đất sét có niên đại khoảng 1900 – 1600 trước Công nguyên đã ghi lại một phát biểu hình học, trong đó ám chỉ ước lượng số π bằng = 3,1250. Hãy ước lượng sai số tuyệt đối và sai số tương đối của giá trị gần đúng này, biết 3,141 < π < 3,142.
Bài 3 trang 26 Toán lớp 10 Tập 2
Bài 3 trang 26 Toán lớp 10 Tập 2: Ta đã biết 1 inch (kí hiệu là in) là 2,54 cm. Màn hình của một chiếc ti vi có dạng hình chữ nhật với độ dài đường chéo là 32 in, tỉ số giữa chiều dài và chiều rộng của màn hình là 16 : 9. Tìm một giá trị gần đúng (theo đơn vị inch) của chiều dài màn hình ti vi và tìm sai số tương đối, độ chính xác của số gần đúng đó.
Bài 2 trang 109 Toán lớp 10 Tập 1
Bài 2 trang 109 Toán lớp 10 Tập 1: Cho số gần đúng a = 6547 với độ chính xác d = 100. Hãy viết số quy tròn của số a và ước lượng sai số tương đối của số quy tròn đó.
Bài 3 trang 109 Toán lớp 10 Tập 1
Bài 3 trang 109 Toán lớp 10 Tập 1: Cho biết
a) Hãy quy tròn đến hàng phần trăm và ước lượng sai số tương đối.
b) Hãy tìm số gần đúng của với độ chính xác 0,003.
c) Hãy tìm số gần đúng của với độ chính xác đến hàng phần chục nghìn.