Phương trình tanx =m | Toán 11 - Cánh diều
Phương trình tanx =m
Dưới đây là công thức Phương trình tanx =m
Phương trình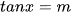 
(3), ĐK:
Với mọi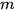 
, tồn tại sao cho với .
Vậy khi , phương trình (3)
Chú ý:
- . Trong đó f(x) và g(x) .
- .
Các công thức liên quan:
Công thức lượng giác đầy đủ
Đầy đủ công thức lượng giác hay nhất, cần thiết cho học sinh, công thức nhân đôi, công thức hạ bậc, công thức tổng thành tích, tích thành tổng, công thức sin tổng, sin hiệu, cos tổng, cos hiệu.