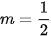Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 2. Hàm số. | Toán 10 - Cánh diều
Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 2. Hàm số.
Dưới đây là công thức Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 2. Hàm số.
Câu 1: (ts Hà Tĩnh 2022-2023): Tìm số thực để đường thẳng có phương trình 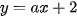 đi qua điểm A(3;8).
đi qua điểm A(3;8).
Lời giải
Vì đường thẳng 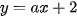 đi qua điểm A(3;8) nên ta có
đi qua điểm A(3;8) nên ta có  .
.
Vậy a=2
Câu 2: (ts Quảng Bình 2022-2023): Tìm tất cả các giá trị của tham số m để đồ thị hàm số  đi qua điểm A(1;4).
đi qua điểm A(1;4).
Lời giải
Để đồ thị hàm số  đi qua điểm
đi qua điểm 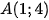 thì:
thì: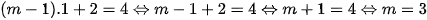
Vậy m=3 là giá trị cần tìm.
Câu 3: (ts Nghệ An 2022-2023) Xác định hệ số a, b của hàm số y= ax + b, biết rằng đồ thị của hàm số đi qua điểm M(-1; 3) và cắt trục tung tại điểm có tung độ bằng -2.
Lời giải
Do đồ thị của hàm số y = ax + b đi qua điểm M(-1; 3) nên 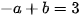 (1)
(1)
Do đồ thị của hàm số y = ax + b cắt trục tung tại điểm có tung độ bằng -2 nên b =-2 (2)
Từ (1), (2) 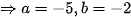 .
.
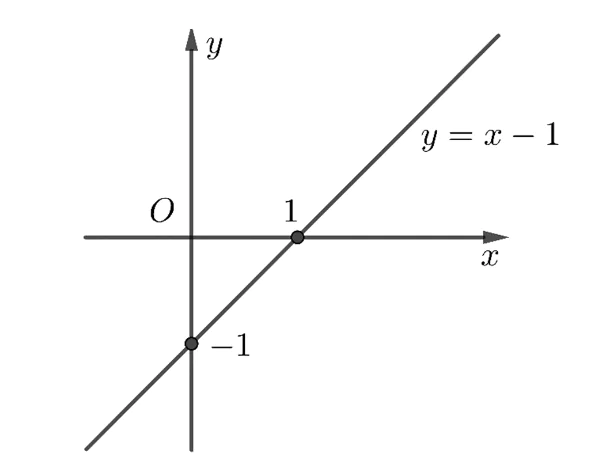
Câu 4: (ts An Giang 2022-2023) Cho hàm số y = x-1 có đồ thị là (d).
a) Vẽ đồ thị (d) trên mặt phẳng tọa độ.
b) Tìm a để (d) tiếp xúc với Parabol (P): 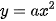 .
.
Lời giải
a) Bảng giá trị:
| x | 0 | 1 |
| y=x-1 | -1 | 0 |
 Đường thẳng d đi qua 2 điểm (0;-1) và (1;0).
Đường thẳng d đi qua 2 điểm (0;-1) và (1;0).
Đồ thị:
b) Hoành độ giao điểm của ( d) và (P) là nghiệm của phương trình: 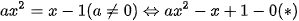
Để d tiếp xúc ( P) thì phương trình (*) có nghiệm duy nhất 
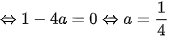
Vậy  .
.
Câu 5: (ts Cao Bằng 2022-2023) Hàm số 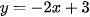 đồng biến hay nghịch biến trên R? Tại sao?
đồng biến hay nghịch biến trên R? Tại sao?
Lời giải
Ta có: a=-2<0 nên hàm số nghịch biến trên R.
Câu 6: (ts Thanh Hóa 2022-2023) Trong mặt phẳng tọa độ Oxy , cho đường thẳng (d) có phương trình 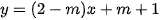 ( m là tham số). Tìm m để đường thẳng ( d ) cắt trục hoành tại điểm có hoành độ bằng 2 .
( m là tham số). Tìm m để đường thẳng ( d ) cắt trục hoành tại điểm có hoành độ bằng 2 .
Lời giải
Vì đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 2 nên đường thẳng (d) đi qua điểm (2;0)
Thay 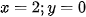 vào phương trình ta được:
vào phương trình ta được: 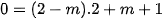
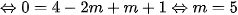
Vậy, với m=5 thì đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 2.
Câu 7: (ts Tây Ninh 2022-2023) Tìm tọa độ giao điểm của đường thẳng (d): y = 2x+6 với trục hoành y = 0.
Lời giải
2x + 6 = 0
⇔ 2x = -6
⇔ x = -3
Vậy giao điểm của đường thẳng (d): y = 2x+6 với trục hoành có tọa độ là (-3;0).
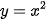 và đường thẳng
và đường thẳng 
b) Tìm tọa độ giao điểm của parabol (P) và đường thẳng (d) bằng phép tính.
Lời giải
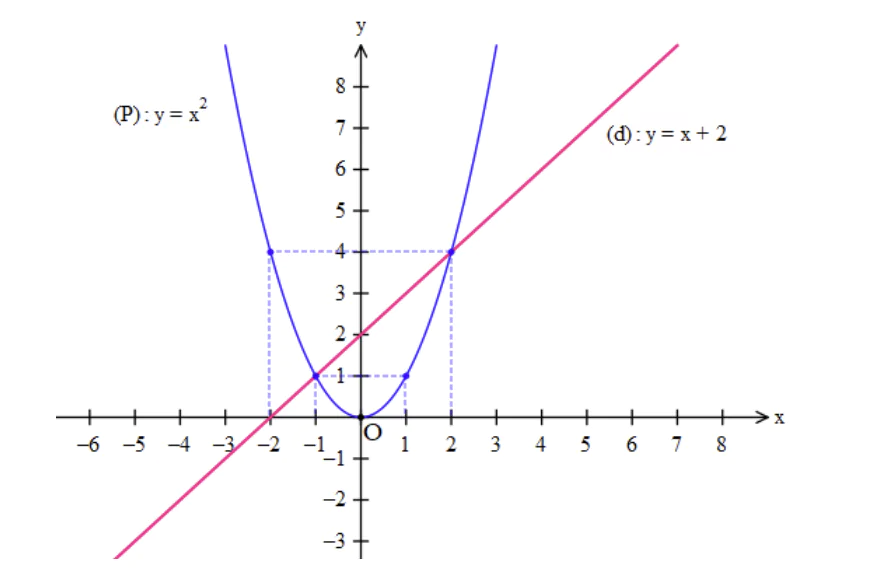
a)
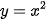
Hệ số a=1>0 nên hàm số đồng biến khi x>0 , nghịch biến khi x<0 và có bề lõm hướng lên trên
Bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
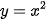 |
4 | 1 | 0 | 1 | 4 |
Parabol (P) là đường cong có đỉnh O(0;0) , qua các điểm
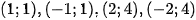
+ Xét đường thẳng (d): y = x+2
Bảng giá trị:
| x | 0 | -2 |
| y=x+2 | 2 | 0 |
 Đường thẳng ( d) cắt trục Ox tại điểm
Đường thẳng ( d) cắt trục Ox tại điểm 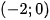 , cắt trục O y tại điểm (0;2)
, cắt trục O y tại điểm (0;2)Vẽ parabol (P) và đường thẳng (d) trên cùng một hệ trục tọa độ Oxy .
b)
Phương trình hoành độ giao điểm của parabol (P) và đường thẳng (d) :
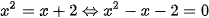
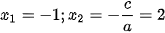
+ Với
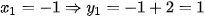
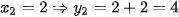
Vậy parabol (P) và đường thẳng (d) cắt nhau tại hai điểm
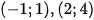
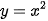 có đồ thị (P) và đường thẳng (d): y= 2x-m (m là tham số).
có đồ thị (P) và đường thẳng (d): y= 2x-m (m là tham số).a) Vẽ (P).
b) Tìm giá trị của m để đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 1.
c) Tìm giá trị của m để (d) cắt (P) tại hai điểm phân biệt có tọa độ
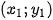 và
và 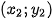 sao cho biểu thức
sao cho biểu thức 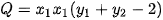 đạt giá trị lớn nhất.
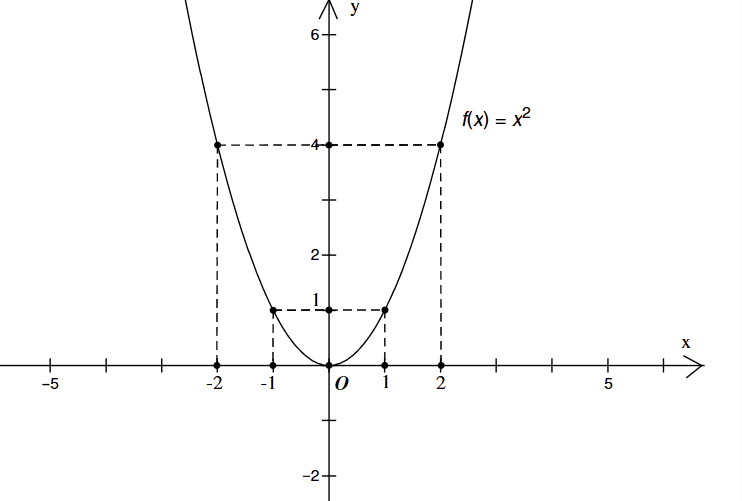
đạt giá trị lớn nhất.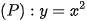 , ta có bảng sau:'
, ta có bảng sau:'| x | -2 | -1 | 0 | 1 | 2 |
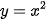 |
4 | 1 | 0 | 1 | 4 |
Vậy đồ thị hàm số 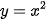 là một Parabol qua
là một Parabol qua 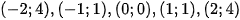 và nhận làm trục đối xứng.
và nhận làm trục đối xứng.
b) Để đường thẳng (d): y = 2x-m cắt trục tung tại điểm có tung độ bằng 1 thì y=1 khi x=0.
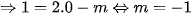 .
.Vậy m=-1 là giá trị cần tìm.
c)
Xét phương trình hoành độ giao điểm của (d) và (P):
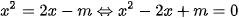 (1);
(1);Để (d) cắt (P) tại hai điểm phân biệt thì (1) phải có hai nghiệm phân biệt
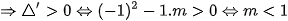
Khi đó phương trình (1) có hai nghiệm phân biệt
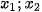 là hoảnh độ giao điểm của (d) và (P),
là hoảnh độ giao điểm của (d) và (P), 
Theo hệ thức Vi-et, ta có:
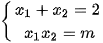
Theo bài ra, ta có:
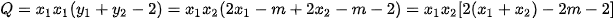
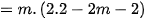
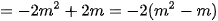
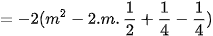
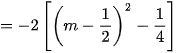
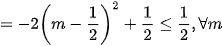
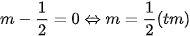
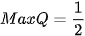 khi
khi