Công thức tổng quát tính thể tích của một khối tứ diện bất kì và các trường hợp đặc biệt | Toán 8 - Chân trời sáng tạo
Công thức tổng quát tính thể tích của một khối tứ diện bất kì và các trường hợp đặc biệt
Dưới đây là công thức Công thức tổng quát tính thể tích của một khối tứ diện bất kì và các trường hợp đặc biệt
Công thức tổng quát: Khối tứ diện ABCD có BC = a, CA = b, AB = c, AD = d, BD = e, CD = f ta có công thức tính thể tích của tứ diện theo sáu cạnh như sau: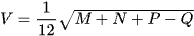 
, trong đó
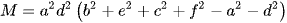
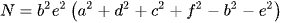
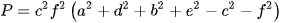
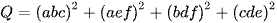
Công thức 1: Khối tứ diện đều
Khối tứ diện đều cạnh a, ta có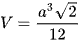 
.
Ví dụ 1: Cho tứ diện đều có chiều cao bằng h. Thể tích của khối tứ diện đã cho là
A.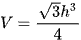 
.
B.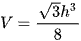 
.
C.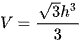 
.
D.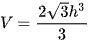 
.
Lời giải
Thể tích tứ diện đều cạnh a là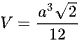 
.
Chiều cao tứ diện đều là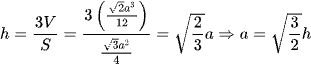 
.
Vì vậy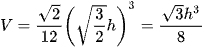 
.
Chọn đáp án B.
Công thức 2: Khối tứ diện vuông (các góc tại một đỉnh của tứ diện là góc vuông)
Với tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB = a, AC = b, AD = c, ta có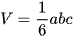 
.
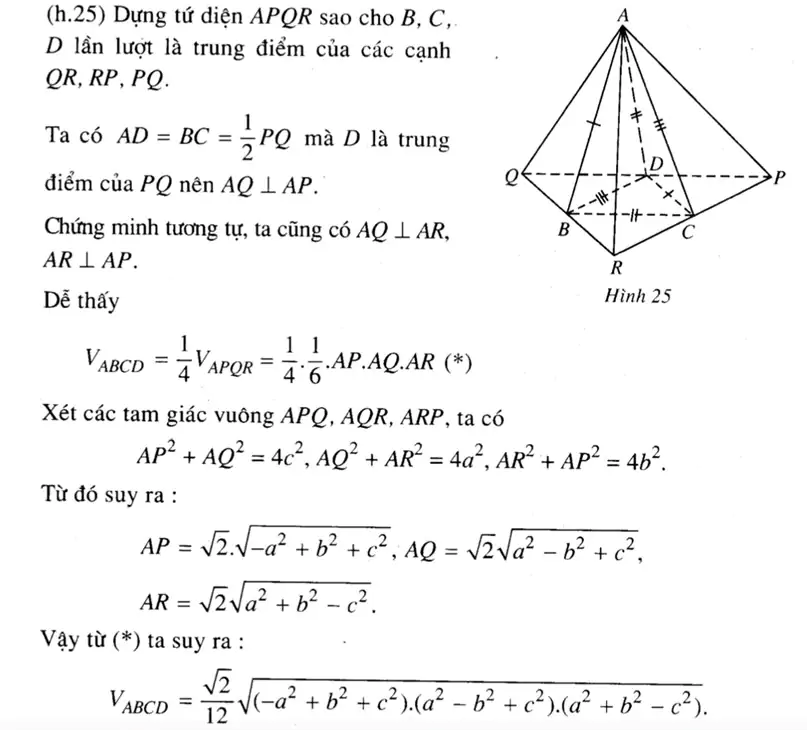
Công thức 3: Khối tứ diện gần đều (các cặp cạnh đối tương ứng bằng nhau)
Với tứ diện ABCD có AB = CD = a, BC = AD = b, AC = BD = c, ta có
.
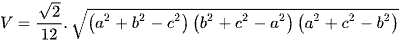Chứng minh
Ví dụ 1: Cho khối tứ diện ABCD có AB = CD = 8, AD = BC = 5 và AC = BD = 7. Thể tích khối tứ diện đã cho bằng
A.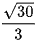 
.
B.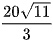 
.
C.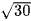 
.
D.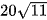 
.
Lời giải
Ta có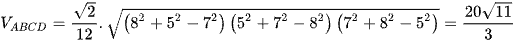 
.
Chọn đáp án B.
Công thức 4: Khối tứ diện có khoảng cách và góc giữa cặp cạnh đối diện của tứ diện
Tứ diện ABCD có AD = a, BC = b, d(AD, BC) = d, (AD, BC) = α, ta có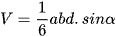 
.
Ví dụ 3: Cho một hình trụ có thiết diện qua trục là một hình vuông cạnh bằng a. Biết rằng AB và CD là hai đường kính tương ứng của hai đáy và góc giữa hai đường thẳng AB và CD bằng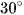 
. Tính thể tích khối tứ diện ABCD.
A.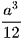 
.
B.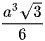 
.
C.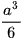 
.
D.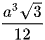 
.
Lời giải
Có h = 2r = a;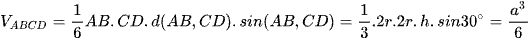 
.
Chọn đáp án C.
Công thức 5: Khối tứ diện biết diện tích hai mặt kề nhau
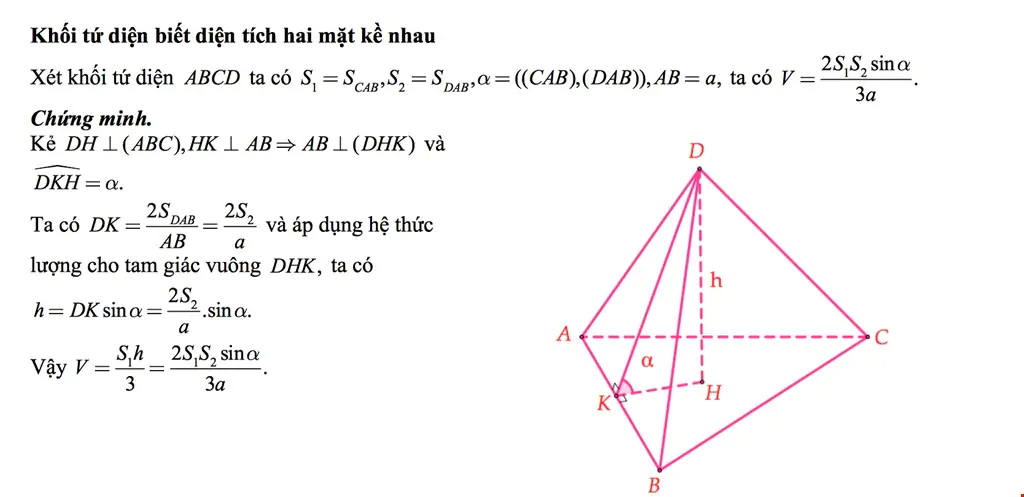
Ví dụ 5: Cho lăng trụ ABC.A'B'C' có diện tích tam giác A'BC bằng 4, khoảng cách từ A đến BC bằng 3, góc giữa hai mặt phẳng (A'BC) và (A'B'C') bằng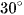 
. Thể tích khối lăng trụ ABC.A'B'C' bằng
A.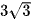 
.
B. 6.
C. 2.
D. 12.
Lời giải
Áp dụng công thức tính thể tích tứ diện cho trường hợp biết góc và diện tích của hai mặt
.
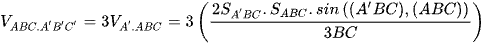
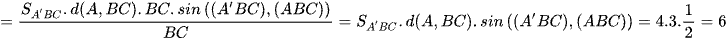Chọn đáp án B.
Công thức 6: Mở rộng cho khối chóp có diện tích mặt bên và mặt đáy
Khối chóp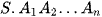 
có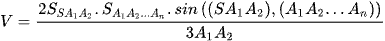 
.
Công thức 7: Khối tứ diện khi biết các góc tại cùng một đỉnh
Ví dụ 1: Cho hình chóp S.ABC có SA = a, SB = 2a, SC = 4a và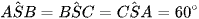 
. Tính thể tích khối chóp S.ABC theo a.
A.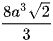 
.
B.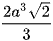 
.
C.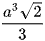 
.
D.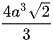 
.
Lời giải
Cách 1: Áp dụng công thức tính thể tích tứ diện theo các góc tại một đỉnh ta có
.
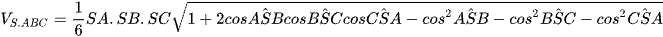
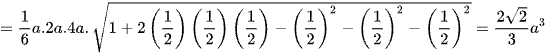Chọn đáp án B.
Cách 2:
