Công thức giải nhanh hình toạ độ không gian Oxyz (Phần 2) | SBT Toán 12 - Cánh diều (SBT)

CÔNG THỨC TÍNH NHANH 7:

PHƯƠNG TRÌNH ĐƯỜNG PHÂN GIÁC CỦA HAI ĐƯỜNG THẲNG CẮT NHAU

Hai đường thẳng 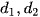 cắt nhau tại điểm  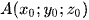và có véctơ chỉ phương lần lượt là .

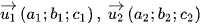Đường thẳng phân giác của góc tạo bởi hai đường thẳng này có véctơ chỉ phương được xác định theo công thức

.

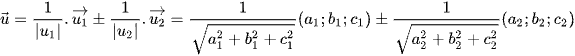Chi tiết có hai phân giác:

Nếu 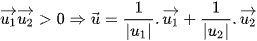 là véctơ chỉ phương của phân giác tạo bởi góc nhọn giữa hai đường thẳng và  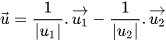là véctơ chỉ phương của phân giác tạo bởi góc tù giữa hai đường thẳng.

Nếu 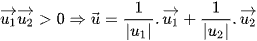 là véctơ chỉ phương của phân giác tạo bởi góc tù giữa hai đường thẳng và  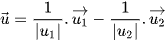là véctơ chỉ phương của phân giác tạo bởi góc nhọn giữa hai đường thẳng.

CÔNG THỨC TÍNH NHANH 8:

KHOẢNG CÁCH GIỮA HAI MẶT PHẲNG SONG SONG

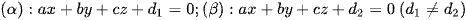 là .

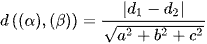CÔNG THỨC TÍNH NHANH 9:

MẶT PHẲNG SONG SONG VÀ CÁCH ĐỀU HAI MẶT PHẲNG

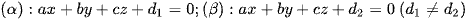 là .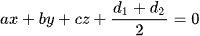

CÔNG THỨC TÍNH NHANH 10:

Tìm toạ độ điểm I thoả mãn đẳng thức véctơ: .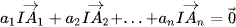

Điểm I được gọi là tâm tỉ cự của hệ điểm .

Toạ độ điểm I được xác định bởi công thức:

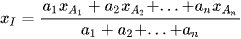
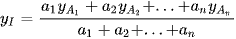
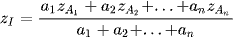
CÔNG THỨC TÍNH NHANH 11:

XÁC ĐỊNH TOẠ ĐỘ TÂM ĐƯỜNG TRÒN NGOẠI TIẾP, TÂM ĐƯỜNG TRÒN NỘI TIẾP, TRỰC TÂM VÀ TRỌNG TÂM CỦA MỘT TAM GIÁC

Dạng 1: Xác định số đo góc của một tam giác

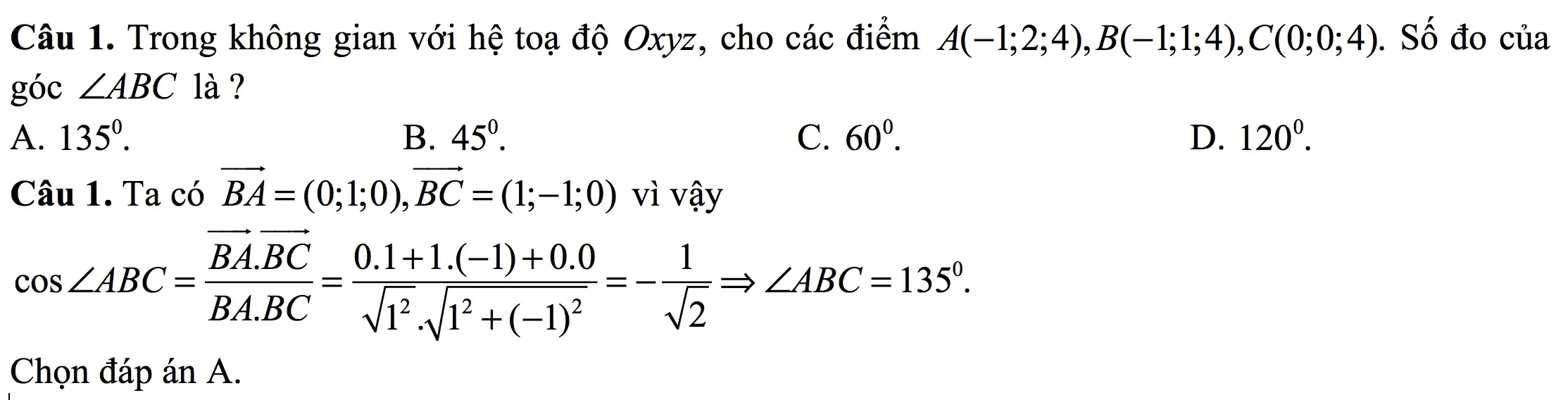
Dạng 2: Xác định tâm đường tròn ngoại tiếp của tam giác 

Tâm ngoại tiếp I của tam giác ABC là điểm thuộc mặt phẳng (ABC) và cách đều các đỉnh của tam giác. Vì vậy để tìm toạ độ tâm ngoại tiếp I của tam giác ABC chúng ta giải hệ phương trình:

.

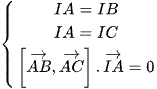*Chú ý. Với bài toán đặc biệt này, các bạn có thể nhận biết tam giác ABC vuông tại A, do đó tâm ngoại tiếp I là trung điểm cạnh huyền BC. 

Dạng 3: Xác định toạ độ trực tâm của tam giác

Trực tâm H là điểm nằm trên mặt phẳng (ABC) và có tính chất vuông góc như sau HA ⊥ BC, HB ⊥ CA, HC ⊥ AB.

Do vậy toạ độ trực tâm H là điểm nằm trên mặt phẳng (ABC) là nghiệm của hệ phương trình .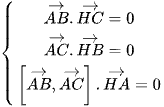

Câu 1: Trong không gian với hệ toạ độ Oxyz, cho các điểm A(2; 3; 1), B(-1; 2; 0), C(1; 1; -2). Tìm toạ độ trực tâm H của tam giác ABC.

A. .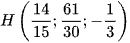

B. .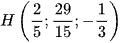

C. .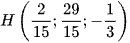

D. .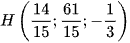

Lời giải

Toạ độ trực tâm H là điểm nằm trên mặt phẳng (ABC) là nghiệm của hệ phương trình

.

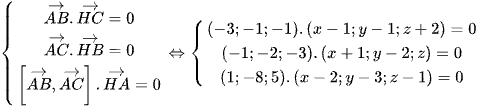
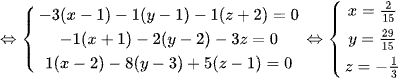Chọn đáp án C. 

CÔNG THỨC TÍNH NHANH 12:

XÁC ĐỊNH TOẠ ĐỘ TÂM VÀ BÁN KÍNH MẶT CẦU NGOẠI TIẾP MỘT TỨ DIỆN VUÔNG