Công thức giải nhanh hình toạ độ không gian Oxyz (Phần 1) | SBT Toán 12 - Cánh diều (SBT)
Công thức giải nhanh hình toạ độ không gian Oxyz (Phần 1)
Dưới đây là công thức Công thức giải nhanh hình toạ độ không gian Oxyz (Phần 1)
CÔNG THỨC TÍNH NHANH 1:
CÁCH XÁC ĐỊNH NHANH TOẠ ĐỘ TÂM ĐƯỜNG TRÒN NỘI TIẾP TAM GIÁC TRONG KHÔNG GIAN OXY
Chú ý: Với I là tâm nội tiếp tam giác ABC ta có đẳng thức véctơ sau đây:
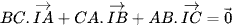
Chuyển qua toạ độ trong không gian Oxyz, ta có thể xác định được nhanh toạ độ điểm I như sau:
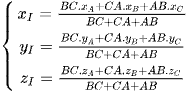 .
.
Ví dụ 1: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC với toạ độ các đỉnh A(1; 1; 1), B(4; 1; 1), C(1; 1; 5). Tìm toạ độ điểm I là tâm đường tròn nội tiếp tam giác ABC.
A. I(-2; -1; -2).
B. I(2; -1; 2).
C. I(2; 1; 2).
D. I(1; 2; 2).
Lời giải
Ta có BC = 5; CA = 4; AB = 3. Do đó
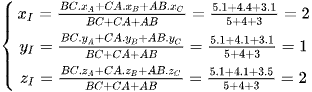 .
.
Vậy I(2; 1; 1).
Chọn đáp án C.
CÔNG THỨC TÍNH NHANH 2:
XÁC ĐỊNH BÁN KÍNH NGOẠI TIẾP TAM GIÁC
Ta đã biết công thức từ chương trình hệ thức lượng Hình học Toán 10 như sau:
Ta biết được rằng 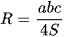 ; trong đó a, b, c là độ dài ba cạnh tam giác và S là diện tích tam giác.
; trong đó a, b, c là độ dài ba cạnh tam giác và S là diện tích tam giác.
Áp dụng trong hình toạ độ không gian Oxyz, ta được
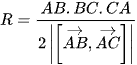 , trong đó tất cả các phép toán có trong công thức trên hoàn toàn bấm trực tiếp bằng máy tính.
, trong đó tất cả các phép toán có trong công thức trên hoàn toàn bấm trực tiếp bằng máy tính.
Câu 1: Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(2; 0; -1), B(1; -2; 3), C(0; 1; 2). Tính bán kính đường tròn ngoại tiếp tam giác ABC.
A. 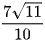 .
.
B. 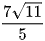 .
.
C. 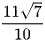 .
.
D. 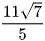 .
.
Lời giải
Ta có 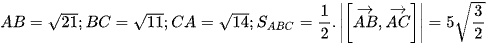 .
.
Vì vậy 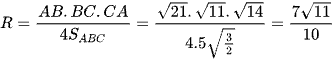 .
.
Chọn đáp án A.
*Chú ý. Thao tác tất cả bằng máy tính, kết quả R ≈
CÔNG THỨC TÍNH NHANH 3:
XÁC ĐỊNH TOẠ ĐỘ HÌNH CHIẾU CỦA MỘT ĐIỂM LÊN CÁC TRỤC TOẠ ĐỘ, MẶT PHẲNG TOẠ ĐỘ
• Xét điểm 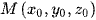 khi đó toạ độ hình chiếu vuông góc của M lên các trục toạ độ Ox, Oy, Oz lần lượt là
khi đó toạ độ hình chiếu vuông góc của M lên các trục toạ độ Ox, Oy, Oz lần lượt là 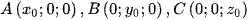 .
.
• Xét điểm 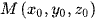 khi đó toạ độ hình chiếu vuông góc của M lên các mặt phẳng toạ độ (Oxy), (Oyz), (Ozx) lần lượt là
khi đó toạ độ hình chiếu vuông góc của M lên các mặt phẳng toạ độ (Oxy), (Oyz), (Ozx) lần lượt là 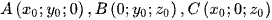 .
.
Ví dụ 1: Viết phương trình mặt phẳng đi qua các hình chiếu vuông góc của M(3; 2; 6) trên các trục toạ độ Ox, Oy, Oz.
Lời giải
Ta có A(3; 0; 0), B(0; 2; 0), C(0; 0; 6) ⇒ 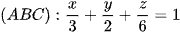 .
.
CÔNG THỨC TÍNH NHANH 4:
XÁC ĐỊNH TOẠ ĐỘ ĐIỂM ĐỐI XỨNG QUA ĐƯỜNG THẲNG, MẶT PHẲNG
• Xét điểm 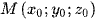 và mặt phẳng (P): ax + by + cz + d = 0.
và mặt phẳng (P): ax + by + cz + d = 0.
Điểm N(x; y; z) đối xứng với M qua mặt phẳng (P) có toạ độ là nghiệm của hệ
 .
.
*Chú ý. Trong hệ phương trình trên hoặc a = 0 hoặc b = 0 hoặc c = 0 thì tương ứng 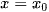 hoặc
hoặc 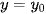 hoặc
hoặc 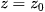 .
.
• Toạ độ điểm N(x; y; z) là hình chiếu vuông góc của điểm 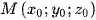 và mặt phẳng (P): ax + by + cz + d = 0 là
và mặt phẳng (P): ax + by + cz + d = 0 là
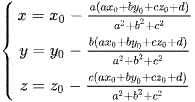 .
.
Ví dụ 1: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P): 2x - 3y + 5z - 4 = 0 và kí hiệu (Q) là mặt phẳng đối xứng với mặt phẳng (P) qua mặt phẳng (Oxz). Hỏi phương trình của mặt phẳng (Q) là?
A. (Q): 2x + 3y + 5z - 4 = 0.
B. (Q): 2x + 3y + 5z + 4 = 0.
C. (Q): 2x - 3y + 5z + 4 = 0.
D. (Q): 2x - 3y + 5z - 4 = 0.
Lời giải
Xét điểm 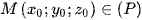 , N(x; y; z) là điểm đối xứng của M qua (Oxz), ta có
, N(x; y; z) là điểm đối xứng của M qua (Oxz), ta có
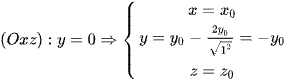 .
.
Thay vào phương trình của (P), ta được 2x - 3(-y) + 5z - 4 = 0 ⇒ (Q): 2x + 3y +5z - 4 = 0.
Chọn đáp án A.
CÔNG THỨC TÍNH NHANH 5:
MẶT PHẲNG PHÂN GIÁC CỦA HAI MẶT PHẲNG GIAO NHAU
Xét hai mặt phẳng 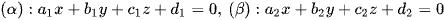 .
.
Khi đó phương trình mặt phẳng phân giác của góc tạo bởi 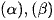 là
là
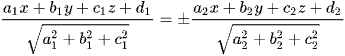 .
.
CÔNG THỨC TÍNH NHANH 6:
VIẾT PHƯƠNG TRÌNH ĐƯỜNG PHÂN GIÁC TRONG VÀ NGOÀI CỦA TAM GIÁC
Xét tam giác ABC, khi đó đường phân giác trong góc A có véctơ chỉ phương là
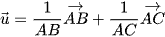 .
.
Ngược lại, đường phân giác ngoài góc A có véctơ chỉ phương là
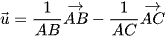 .
.

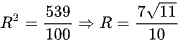 .
.