Giải bài tập Bài 3 trang 66 Chuyên đề Toán 11 | Chuyên đề học tập Chân Trời Sáng Tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 3 trang 66 Chuyên đề Toán 11. Bài 3. Bài toán tìm đường đi ngắn nhất.. Chuyên đề học tập Chân Trời Sáng Tạo
Đề bài:
Bài 3 trang 66 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ đỉnh S đến T trong đồ thị trọng số ở Hình 17.

Đáp án và cách giải chi tiết:
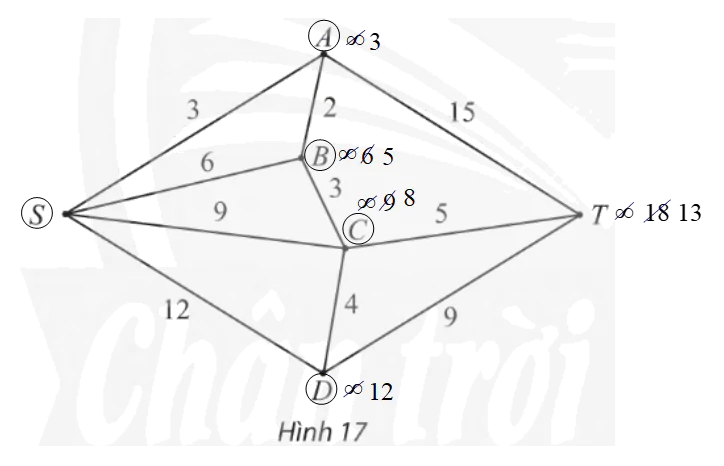
– Gán nhãn cho S bằng 0 (tức là, nS = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh A.
– Tại các đỉnh kề với S, gồm A, B, C, D. ta có:
⦁ nA = nS + wSA = 0 + 3 = 3.Vì 3 < ∞ nên ta đổi nhãn của A thành 3.
⦁ nB = nS + wSB = 0 + 6 = 6.Vì 6 < ∞ nên ta đổi nhãn của B thành 6.
⦁ nC = nS + wSC = 0 + 9 = 9.Vì 9 < ∞ nên ta đổi nhãn của C thành 9.
⦁ nD = nS + wSD = 0 + 12 = 12.Vì 12 < ∞ nên ta đổi nhãn của D thành 12.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là A nên ta khoanh tròn đỉnh A (đỉnh gần S nhất, chỉ tính các đỉnh khác S).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh A gồm B, T, ta có:
⦁ nB = nA + wAB = 3 + 2 = 5.Vì 5 < 6 (6 là nhãn hiện tại của B) nên ta đổi nhãn của B thành 5.
⦁ nT = nA + wAT = 3 + 15 = 18.Vì 18 < ∞ nên ta đổi nhãn của T thành 18.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần S thứ hai).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh B chỉ có đỉnh C, ta có:
nC = nB + wBC = 5 + 3 = 8.Vì 8 < 9 (9 là nhãn hiện tại của C) nên ta đổi nhãn của C thành 8.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là đỉnh C nên ta khoanh tròn đỉnh C (đỉnh gần S thứ ba).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh C gồm D, T, ta có:
⦁ nD = nC + wCD = 8 + 4 = 12.Vì 12 cũng là nhãn hiện tại của D nên ta giữ nguyên nhãn của D là 12.
⦁ nT = nC + wCT = 8 + 5 = 13.Vì 13 < 18 (18 là nhãn hiện tại của T) nên ta đổi nhãn của T thành 13.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là đỉnh D nên ta khoanh tròn đỉnh D (đỉnh gần S thứ tư).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh D chỉ còn đỉnh T, ta có:
nT = nD + wDT = 12 + 9 = 21.Vì 21 > 13 (13 là nhãn hiện tại của T) nên ta giữ nguyên nhãn của T là 13.
Lúc này, ta thấy chỉ còn đỉnh T nên ta khoanh tròn đỉnh T (đỉnh gần S thứ năm).
– Nhìn lại các bước trên, ta thấy:
nT = 13 = nC + wCT
= nB + wBC + wCT
= nA + wAB + wBC + wCT
= nS + wSA + wAB + wBC + wCT
= wSA + wAB + wBC + wCT
= lSABCT.
Vậy SABCT là đường đi ngắn nhất từ S đến T, với độ dài bằng 13.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 59 Chuyên đề Toán 11
Khởi động trang 59 Chuyên đề Toán 11: Phần mềm chỉ đường thường chỉ ra đường đi ngắn nhất khi người dùng muốn tìm đường đi từ một địa điểm đến một địa điểm khác.
Làm thế nào để tìm ra đường đi đó?

Khám phá 1 trang 59 Chuyên đề Toán 11:
Khám phá 1 trang 59 Chuyên đề Toán 11: Để biểu diễn các con đường nối các giao lộ cùng với độ dài của chúng như sơ đồ ở Hình 1, một học sinh đã vẽ đồ thị như Hình 2. Chỉ ra các cạnh và số biểu diễn độ dài con đường còn thiếu trong Hình 2.

Khám phá 2 trang 61 Chuyên đề Toán 11
Khám phá 2 trang 61 Chuyên đề Toán 11: Cho đồ thị có trọng số như Hình 6.

a) Tìm tất cả các đường đi từ A đến T (đi qua mỗi đỉnh nhiều nhất một lần) và tính độ dài của mỗi đường đi đó.
b) Từ đó, tìm đường đi ngắn nhất từ A đến T.
Thực hành 1 trang 61 Chuyên đề Toán 11
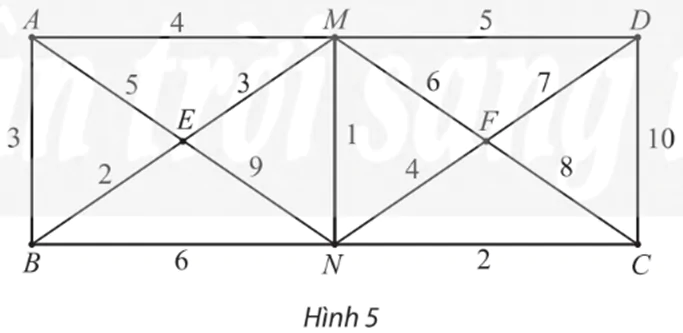
Thực hành 1 trang 61 Chuyên đề Toán 11: Cho đồ thị có trọng số như Hình 5.
a) Chỉ ra trọng số của các cạnh AE, MN, CN.
b) Tính độ dài của các đường đi ABEN, EMFNE.
c) Chỉ ra ba đường đi khác nhau từ A đến D và tính độ dài của chúng.
d) Đường đi EMF có phải là đường đi ngắn nhất từ E đến F không?
Thực hành 2 trang 65 Chuyên đề Toán 11
Thực hành 2 trang 65 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ đỉnh A đến đỉnh I trong đồ thị có trọng số ở Hình 14.

Vận dụng trang 65 Chuyên đề Toán 11
Vận dụng trang 65 Chuyên đề Toán 11: Trong đồ thị có trọng số ở Hình 15, mỗi cạnh biểu diễn một tuyến xe buýt giữa hai bến trong các bến xe A, B, C, D, E và F, trọng số của mỗi cạnh biểu diễn thời gian tính bằng giờ của tuyến xe buýt tương ứng. Một người cần ít nhất bao nhiêu thời gian để di chuyển từ bến A đến bến C bằng xe buýt của các tuyến trên? Biết rằng thời gian tại bến để chuyển tiếp từ tuyến này qua tuyến kia là không đáng kể.

Bài 1 trang 66 Chuyên đề Toán 11
Bài 1 trang 66 Chuyên đề Toán 11: Cho đồ thị có trọng số như Hình 16.

a) Tính độ dài các đường đi ABCD, MBNCP.
b) Chỉ ra ba đường đi khác nhau từ M đến N và tính độ dài của chúng.
c) MBC có phải là đường đi ngắn nhất từ M đến C không?
Bài 2 trang 66 Chuyên đề Toán 11
Bài 2 trang 66 Chuyên đề Toán 11: Bảng 2 cho biết thời gian di chuyển tính bằng giờ của các tuyến xe buýt giữa các bến xe A, B, C, D, E (số nằm tại ô giao của hàng và cột là số giờ cần để xe buýt đi từ bến này đến bến kia, dấu x biểu thị giữa hai bến này không có tuyến xe buýt). Hãy vẽ một đồ thị có trọng số biểu diễn các tuyến xe buýt cùng thời gian di chuyển của mỗi tuyến.

Bài 4 trang 66 Chuyên đề Toán 11
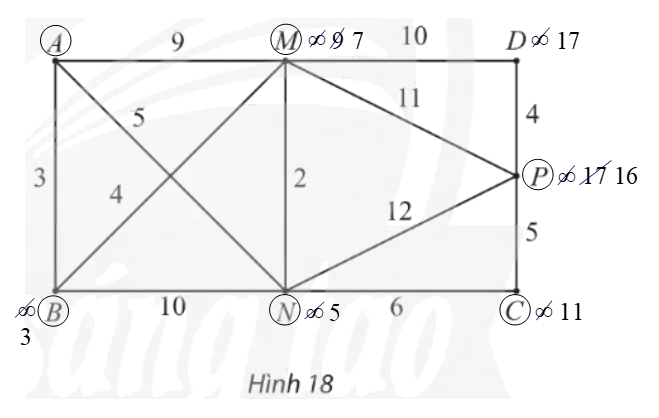
Bài 4 trang 66 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ đỉnh A đến P trong đồ thị có trọng số ở Hình 18.
Bài 5 trang 66 Chuyên đề Toán 11
Bài 5 trang 66 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ đỉnh A đến từng đỉnh (khác A) trong đồ thị có trọng số ở Hình 19.
