Tổng hợp tất cả các công thức tính nhanh Tỷ số thể tích khối đa diện | Toán 8 - Chân trời sáng tạo
Tổng hợp tất cả các công thức tính nhanh Tỷ số thể tích khối đa diện
Dưới đây là công thức Tổng hợp tất cả các công thức tính nhanh Tỷ số thể tích khối đa diện
Công thức 1: Hai khối chóp chung đỉnh và chung mặt phẳng đáy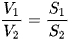 
.
Câu 1: Cho khối chóp S.ABC có thể tích V. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB và V' là thể tích khối chóp S.MNP. Tính tỉ số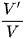 
.
A.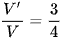 
.
B.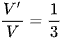 
.
C.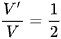 
.
D.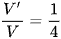 
.
Lời giải
Ta có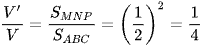 
.
Chọn đáp án D.
Câu 2: Cho khối chóp S.ABCD có thể tích V. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA và V' là thể tích khối chóp S.MNPQ. Tính tỉ số .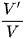
A.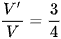 
.
B.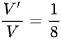 
.
C.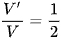 
.
D.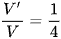 
.
Lời giải
Ta có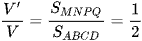 
.
Chọn đáp án C.
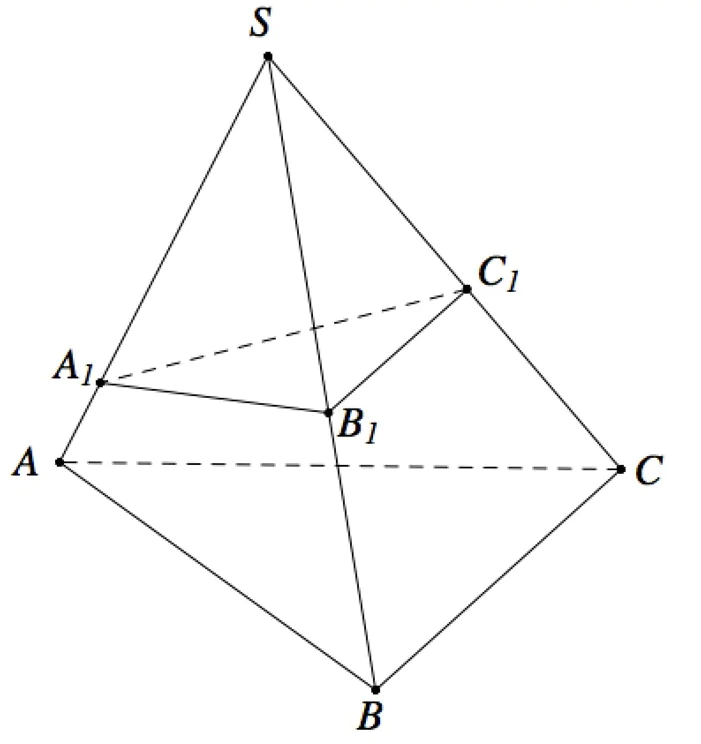
Công thức 2: Công thức Simson (tỷ số thể tích) cho khối chóp tam giác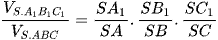 
.
Công thức 3: Cắt khối chóp bởi mặt phẳng song song với đáy sao cho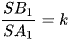 
thì 
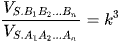(đây là trường hợp đặc biệt cho hai khối đa diện đồng dạng tỷ số k).
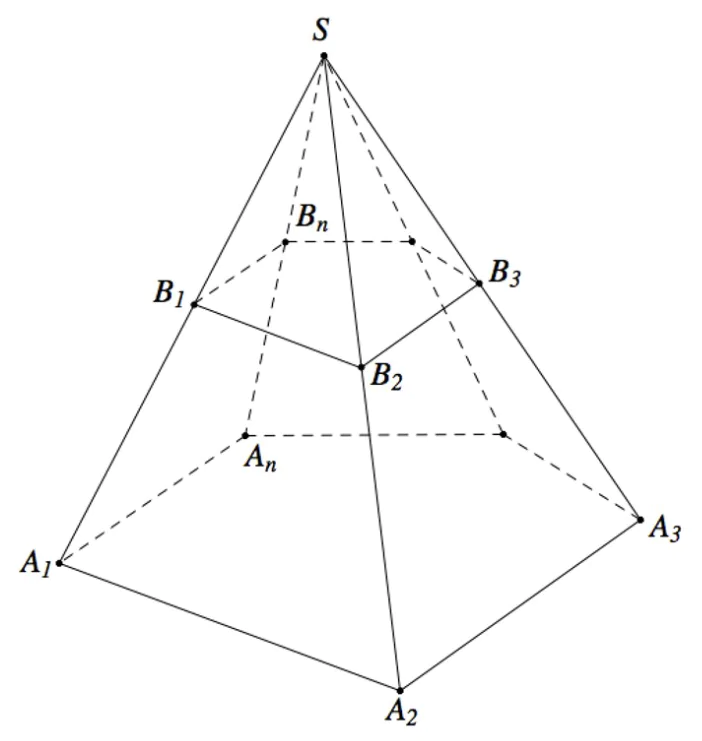
Công thức 4: Mặt phẳng cắt các cạnh của khối lăng trụ tam giác ABC.A'B'C' lần lượt tại M, N, P sao ch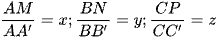o 
ta có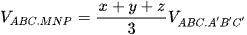 
.
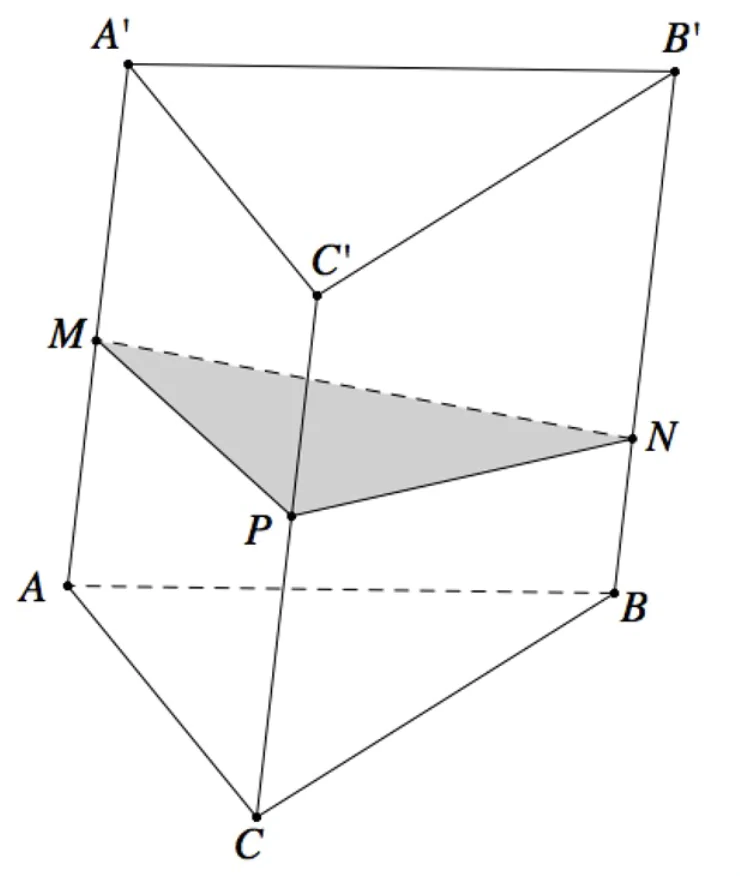
Ví dụ 1: Cho khối lăng trụ tam giác ABC.A'B'C' có thể tích V. Các điểm M, N lần lượt thuộc các cạnh BB', CC' sao cho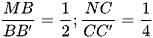 
. Thể tích của khối chóp tứ giác A.BMNC là?
A. 
.
B. 
.
C.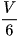 
.
D.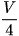 
.
Lời giải
Ta có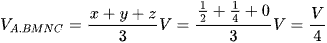 
.
Chọn đáp án D.
Công thức 5: Mặt phẳng cắt các cạnh của khối hộp ABCD.A'B'C'D' lần lượt tại M, N, P, Q sao ch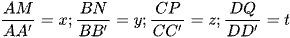o 
ta có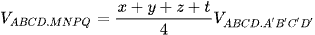 
và x + z = y + t.
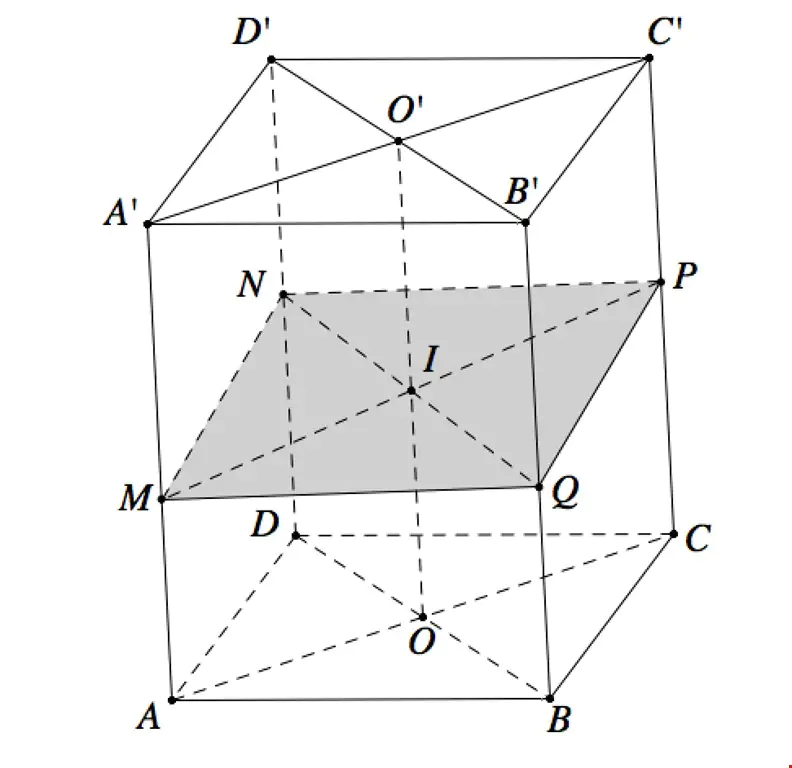
Ví dụ 1: Cho hình lập phương ABCD.A'B'C'D' cạnh 2a, gọi M là trung điểm của BB′ và P thuộc cạnh DD' sao cho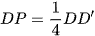 
. Mặt phẳng (AMP) cắt CC' tại N. Thể tích khối đa diện AMNPQBCD bằng
A.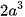 
.
B.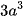 
.
C.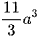 
.
D.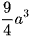 
.
Lời giải
Thể tích khối lập phương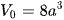 
. Có 
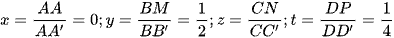và x + z = y + t ⇔ 
.
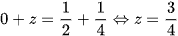Khi đó 
.
Chọn đáp án B.
Công thức 6: Mặt phẳng cắt các cạnh của khối chóp tứ giác S.ABCD có đáy là hình bình hành lần lượt tại M, N, P, Q sao ch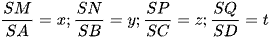o 
ta có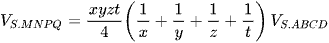 
và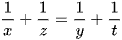 
.
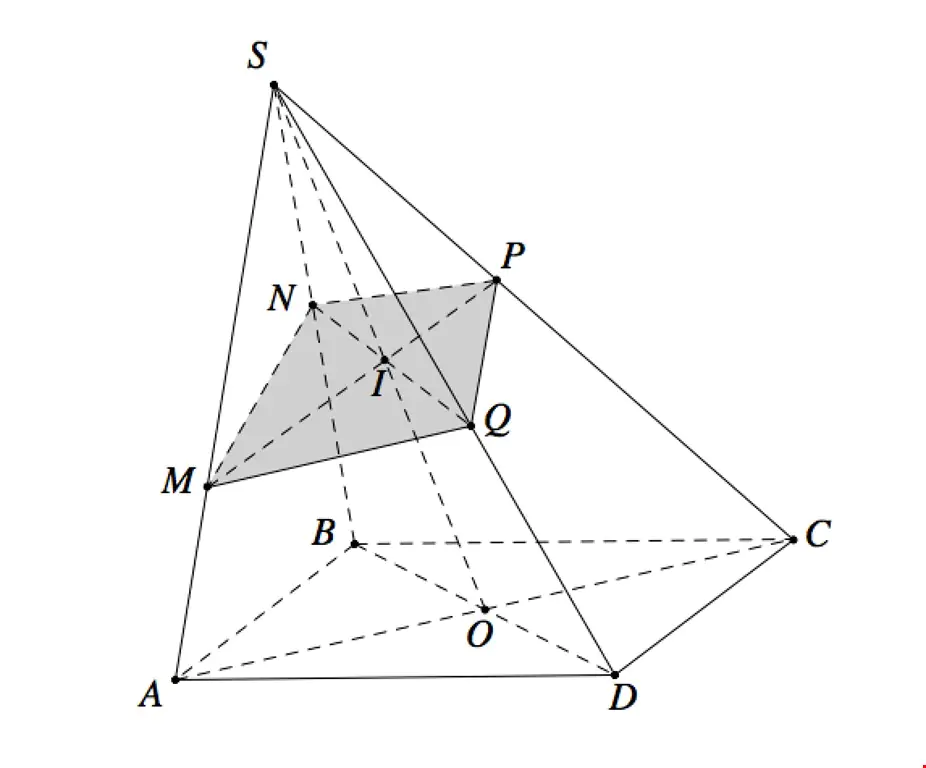
Ví dụ 1: Cho hình chóp S.ABCD có thể tích V với đáy ABCD là hình bình hành. Mặt phẳng qua A, M, P cắt cạnh SC tại N với M, P là các điểm thuộc các cạnh SB, SD sao cho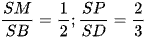 
. Tính thể tích khối đa diện ABCD.MNP.
A.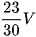 
.
B.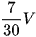 
.
C.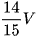 
.
D.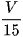 
.
Lời giải
Ta có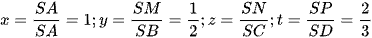 
và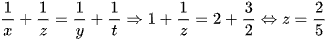 
.
Do đó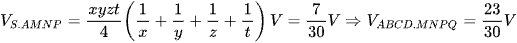 
.
Chọn đáp án A.
Công thức 7: Hai khối đa diện đồng dạng với tỷ số k có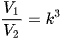 
.
Ví dụ 1: Cho khối tứ diện ABCD có thể tích V. Gọi V' là thể tích của khối tứ diện có bốn đỉnh là trọng tâm các mặt của khối tứ diện ABCD. Tính tỷ số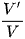 
.
A.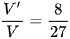 
.
B.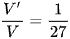 
.
C.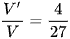 
.
D.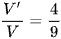 
.
Lời giải
Gọi A', B', C', D' lần lượt là trọng tâm các mặt (BCD), (ACD), (ABD), (ABC). Ta có
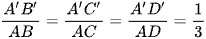. Khối tứ diện A'B'C'D' đồng dạng với khối tứ diện ABCD theo tỉ số 
.
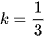Do đó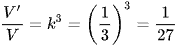 
.
Chọn đáp án B.