Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 8. Hình học. | Toán 9 - Cánh diều
Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 8.Hình học.
Dưới đây là công thức Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 8. Hình học.
Câu 1: Cho tam giác nhọn ABC, các đường cao AE, BF và CN cắt nhau tại H (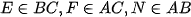
).
a) Chứng minh tứ giác CEHF nội tiếp.
b) Kéo dài FE cắt đường tròn đường kính BC tại M . Chứng minh BM=BN .
c) Biết AH=BC. Tính số đo góc A của tam giác ABC .
Lời giải
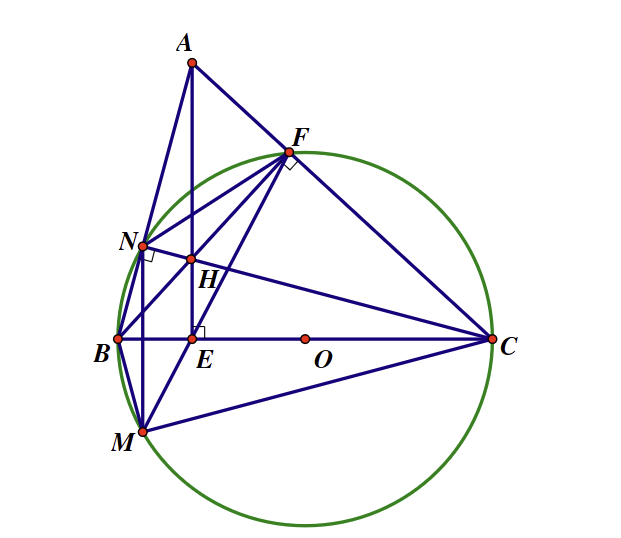
a) Ta có: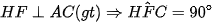 
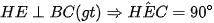
Xét tứ giác CEHF có: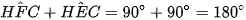 
mà hai góc này đối nhau 
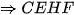là tứ giác nội tiếp.
b) Ta có: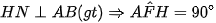 
Xét tứ giác AFHN có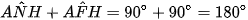 
mà hai góc này đối nhau 
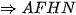là tứ giác nội tiếp.
(2 góc nội tiếp cùng chắn cung HN) (1)
Tứ giác HECF nội tiếp(cmt)
( 2 góc nội tiếp cùng chắn cung HE) (2)
Ta có: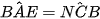 
(2 góc cùng phụ với 
) 
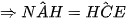(3)
Từ (1), (2), (3) suy ra 
hay 
Xét (O) có:
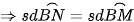(hai góc nội tiếp bằng nhau hai cung chắn bằng nhau)
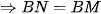(hai cung chắn bằng nhau hai dây bằng nhau) (đpcm)
c) Xét hai tam giác vuông FAH và FBH ta có:
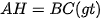
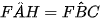(vì cùng phụ với góc 
)
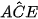Vậy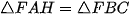 
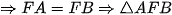vuông cân
Vậy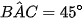 
.
Câu 2: Từ điểm M nằm ngoài đường tròn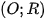 
kẻ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC không đi qua tâm O (điểm B nằm giữa hai điểm M và C). Gọi H là trung điểm của BC . Đường thẳng OH cắt 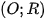tại hai điểm N, K (trong đó điểm K thuộc cung BAC) . Gọi D là giao điểm của AN và BC
a) Chứng minh tứ giác AKHD nội tiếp.
b) Chứng minh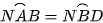 
và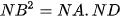 
c) Chứng minh rằng khi đường tròn 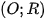và điểm M cố định, đồng thời cát tuyến MBC thay đổi, thì điểm D nằm trên đường tròn cố định.
Lời giải
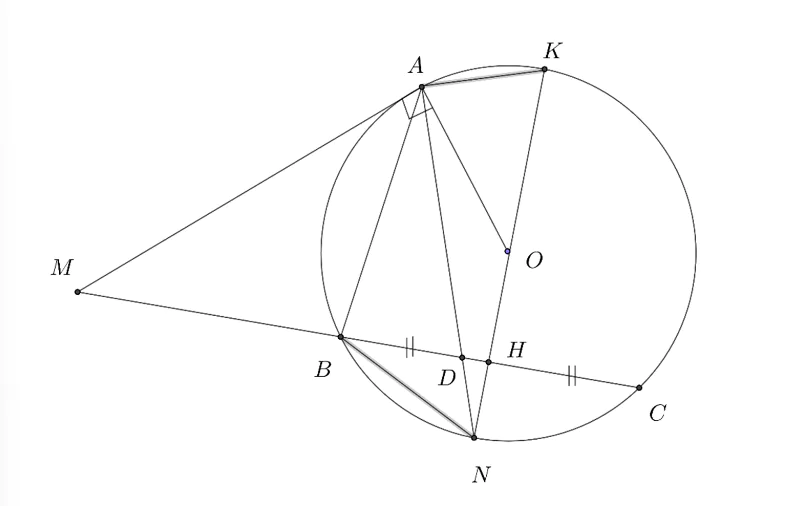
a) Xét 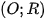) có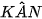 
là góc nội tiếp chắn nửa đường tròn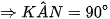 
Có BC là dây không đi qua tâm, H là trung điểm của BC, KN là đường kính của đường tròn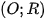 
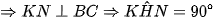
Tứ giác AKHD có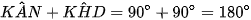 
mà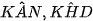 
là 2 góc đối diện
Tứ giấc AKHD là tứ giác nội tiếp
b) Xét 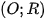có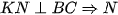 
là điểm chính giữa cung BC
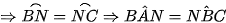(2 góc nội tiếp cùng chắn hai cung bằng nhau)
Xét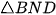 
và 
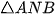có:
đồng dạng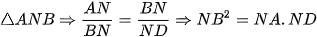 
c) Tứ giác AKHD có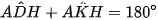 
(hai góc đối nhau) (1)
Mà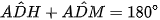 
(2 góc kề bù) (2)
Nên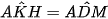 
Mặt khác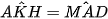 
( góc nội tiếp cùng chắn cung AN)
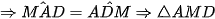cân tại M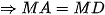 
Mà điểm M và 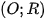cố định 
tiếp tuyến MA cố định và độ dài MA không đổi
D thuộc đường tròn tâm M bán kính MA.
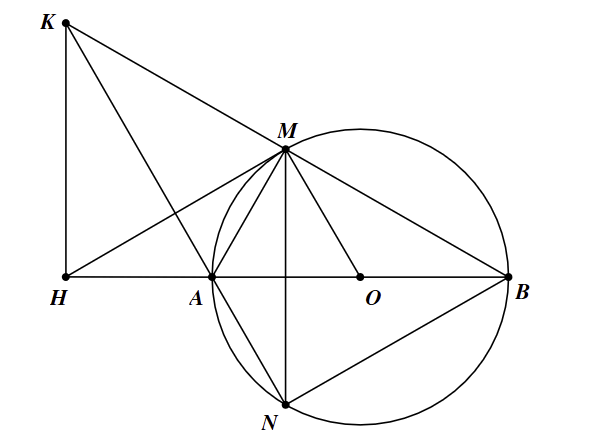
Câu 3: Cho đường tròn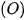 
đường kính AB. Dây cung MN vuông góc với AB, (AM<BM). Hai đường thẳng BM và NA cắt nhau tại K. Gọi H là chân đường vuông góc kẻ từ K đến đường thẳng AB .
a) Chứng minh tứ giác AHKM nội tiếp.
b) Chứng minh rằng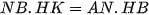 
c) Chứng minh HM là tiếp tuyến của đường tròn .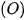
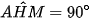(vì 
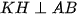) và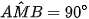 
(góc nội tiếp chắn nửa đường tròn) 
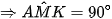(kề bù với 
)
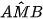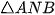và 
có: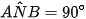
(góc nội tiếp chắn nửa đường tròn)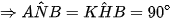 
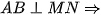A là điểm chính giữa cung MN (quan hệ vuông góc giữa đường kính và dây) 
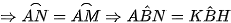(2 góc nội tiếp chắn 2 cung bằng nhau)
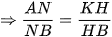
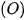tại m, ta phải chứng minh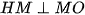 
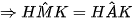(2 góc nội tiếp cùng chắn cung HK)
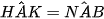(2 góc đối đỉnh)
(
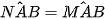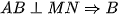là điểm chính giữa cung MN, hai góc nội tiếp chắn hai cung bằng nhau)
(
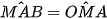cân tại O)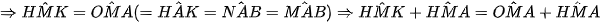
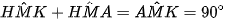(kề bù với 
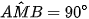, góc nội tiếp chắn nửa đường tròn)
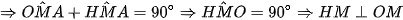tại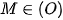 
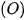HM là tiếp tuyến của .a) Chứng minh tứ giác BMEF nội tiếp
b) Chứng minh tia MA là phân giác của góc CMD
c) Chứng minh
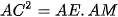
d) Gọi I là giao điểm của hai đường thẳng MD và AB, N là giao điểm của hai đường thẳng AM và BC. Chứng minh tâm đường tròn ngoại tiếp tam giác CEN nằm trên đường thẳng CI.
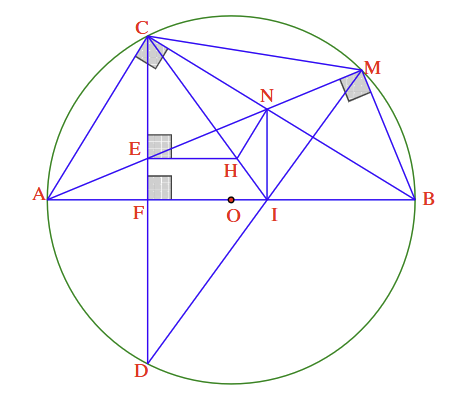
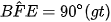
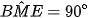(góc nội tiếp chắn nửa đường tròn)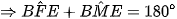
Mà hai góc
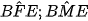nằm ở vị trí đối nhau nên tứ giác BMEF nội tiếpb) Ta có
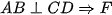là trung điểm của CD (mối liên hệ giữa đường kính và dây cung)=> AB là đường trung trực của
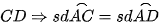
Ta có
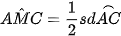và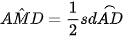 
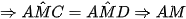là phân giác của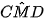 
c) Xét
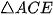và 
có:
chung
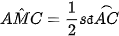và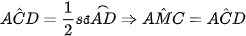 
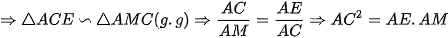
d) Trên CI lấy điểm H sao cho HE vuông góc với CD
Cần chứng minh tứ giác CEHN nội tiếp đường tròn đường kính CH, ta đi chứng minh
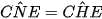
Ta có:
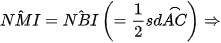tứ giác BMNI nội tiếp
tứ giác ACNI nội tiếpTa có:
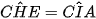(đồng vị); 
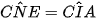(cùng chắn cung AC )
tứ giác CEHN nội tiếpMà
là đường kính=> tâm đường tròn ngoại tiếp tam giác CEN nằm trên CI .