Cấp số nhân | Toán 11 - Cánh diều
Cấp số nhân
Dưới đây là công thức Cấp số nhân
I. Định nghĩa
Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
Nếu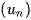 
là cấp số nhân với công bội q, ta có công thức truy hồi:
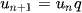với 
.
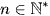Đặc biệt:
-
Khi q = 0, cấp số nhân có dạng
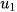, 0, 0, ..., 0, ...
-
Khi q = 1, cấp số nhân có dạng
-
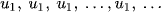
Khi
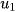= 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0, ..., 0, ...
II. Số hạng tổng quát
Định lí 1. Nếu cấp số nhân có số hạng đầu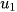 
và công bội q thì số hạng tổng quát 
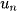được xác định bởi công thức
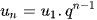với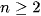 
.
III. Tính chất
Định lí 2. Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là
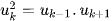, với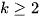 
.
IV. Tổng n số hạng đầu tiên của cấp số nhân
Định lí 3. Cho cấp số nhân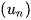 
với công bội 
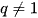. Đặt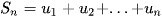 
. Khi đó, 
.
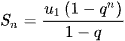Chú ý: Nếu q = 1 thì cấp số nhân là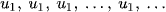 
Khi đó 
.
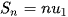CÁC DẠNG BÀI TẬP THƯỜNG GẶP
DẠNG 1: CHỨNG MINH MỘT DÃY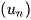 
LÀ CẤP SỐ NHÂN.
A. Phương pháp giải
Chứng minh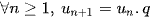 
trong đó q là số không đổi.
Nếu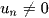 
với mọi 
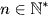thì ta lập tỉ số T = 
.
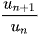* T là hằng số thì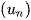 
là cấp số nhân có công bội q = T.
* T phụ thuộc vào n thì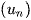 
không là cấp số nhân.
DẠNG 2: XÁC ĐỊNH SỐ HẠNG ĐẦU CÔNG BỘI, XÁC ĐỊNH SỐ HẠNG THỨ K, TÍNH TỔNG CỦA N SỐ HẠNG ĐẦU TIÊN:
A. Phương pháp giải
Dựa vào giả thuyết, ta lập một hệ phương trình chứa công bội q và số hạng đầu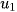 
, giải hệ phương trình này tìm được q và 
.
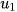Để xác định số hạng thứ k, ta sử dụng công thức: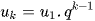 
.
Để tính tổng của n số hạng, ta sử dụng công thức: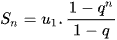 
. Nếu q = 1 thì 
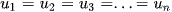, do đó 
.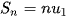