Cấp số cộng | Toán 11 - Cánh diều
Cấp số cộng
Dưới đây là công thức Cấp số cộng
1. Định nghĩa: Cấp số cộng là một dãy số (vô hạn hay hữu hạn) mà trong đó, kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số hạng đứng ngay trước nó và một số d không đổi, nghĩa là:
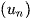là cấp số cộng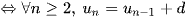 
Số d được gọi là công sai của cấp số cộng.
Phương pháp giải
Để chứng minh dãy số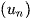 
là một cấp số cộng, ta xét A = 
.
-
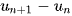Nếu A là hằng số thì
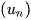là một cấp số cộng với công sai d = A.
-
Nếu A phụ thuộc vào n thì
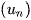không là cấp số cộng.
2. Định lý 1: Nếu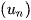 
là một cấp số cộng thì kể từ số hạng thứ hai, mỗi số hạng ( trừ số hạng cuối đối với cấp số cộng hữu hạn) đều là trung bình cộng của hai số hạng đứng kề nó trong dãy, tức là 
.
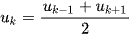Hệ quả: Ba số a,b,c (theo thứ tự đó) lập thành một cấp số cộng 
a + c = 2b.
3. Định lý 2: Nếu một cấp số cộng có số hạng đầu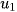 
và công sai d thì số hạng tổng quát 
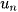của nó được xác định bởi công thức sau: 
.
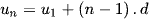4. Định lý 3: Giả sử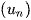 
là một cấp số cộng có công sai d. Gọi 
.
(
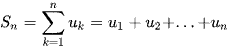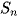là tổng của n số hạng đầu tiên của cấp số cộng). Ta có:
.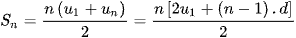