Bài tập thực tế Toán 10. Phương pháp toạ độ trong mặt phẳng. | SBT Toán 12 - Kết nối tri thức (SBT)

Câu 1: Một trò chơi trên máy tính đang mô phỏng một vùng biển có hai hòn đảo nhỏ có toạ độ 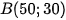và 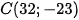. Một con tàu đang neo đậu tại điểm 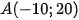. Cho biết một đơn vị trên hệ trục toạ độ tương ứng với 1km . Tính khoảng cách từ con tàu đến mỗi hòn đảo.

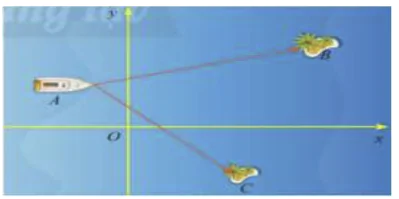
Vì con tàu đang neo đậu tại điểm 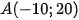 và hòn đảo có toạ độ  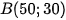nên khoảng cách từ con tàu đến hòn đảo B là 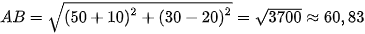(km)
Vì con tàu đang neo đậu tại điểm 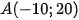 và hòn đảo  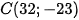nên khoảng cách từ con
tàu đến hòn đảo C là 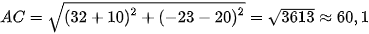(km).

Câu 2: Một trò chơi đua ô tô vượt sa mạc trên máy tính đã xác định được một hệ trục tọa độ Oxy (tham khảo hình ảnh dưới đây). Cho biết một ô tô chuyển động thẳng đều từ điểm M(1;1) với vectơ vận tốc 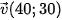. Tìm tọa độ của xe tại thời điểm t=4s.

Lời giải

Hành trình di chuyển của ô tô vượt sa m ạc được thể hiện trên đường thẳng ∆ đi qua điểm M(1;1) và nhận vectơ 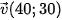 làm vectơ chỉ phương.
Khi đó phương trình tham số của đường thẳng ∆ là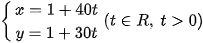

Vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 4 giây là điểm 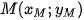 được xác định bởi: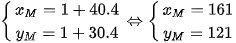

Vậy sau khi vượt sa mạc 4 giây thì ô tô ở vị trí điểm 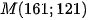 trên mặt phẳng tọa độ.

Câu 3: Một người đang viết chương trình cho trò chơi bóng đá robot đã xác định được một hệ trục tọa độ Oxy . Gọi 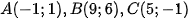 là ba vị trí trên màn hình. Tính khoảng cách từ A đến đường thẳng BC.

Lời giải
Gọi ∆ là đường thẳng đi qua 2 vị trí 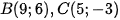của robot. Đường thẳng ∆ có một vecto chỉ phương là  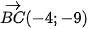nên có một vecto pháp tuyến 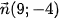. Khi đó phương trình tổng quát của đường thẳng ∆ là  .
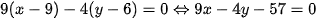Kết luận: Khoảng cách từ A đến đường thẳng BC là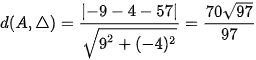

Câu 4: Một chiếc phi cơ bắt đầu chạy trên đường băng 300m rồi cất cánh, độ cao của nó tăng với vận tốc 14 m/s, còn khoảng cách trên mặt đất tăng với vận tốc 64 m/s. Chọn hệ trục tọa độ với gốc tọa độ đặt ở vị trí ban đầu của máy bay, trục hoành thể hiện sự di chuyển trên mặt đất, trục tung thể hiện độ cao của phi cơ; gốc thời gian tính tại thời điểm phi cơ cất cánh.

a. Viết phương trình đường thẳng biểu diễn quỹ đạo bay của phi cơ kể từ thời điểm máy bay bắt
đầu cất cánh.
b. Tìm vị trí của phi cơ sau 15 giây cất cánh.

Lời giải 

a. Vì chiếc phi cơ bắt đầu chạy trên đường băng 300m rồi cất cánh nên tại vị trí máy bay bắt đầu cất cánh thì chiếc phi cơ đang ở vị trí điểm 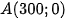. Sau 1 giây đầu tiên thì chiếc phi cơ đang ở vị trí điểm 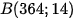. Khi đó đường thẳng ∆ biểu diễn quỹ đạo bay của phi cơ đi qua hai điểm  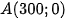và 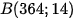. Đường thẳng ∆ có một vecto chỉ phương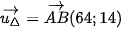
Khi đó ∆ có một vecto pháp tuyến là 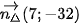 nên có phương trình tổng quát là

b. Sau 15 giây thì chiếc phi cơ đang ở độ cao  , còn nếu xét theo sự di chuyển trên mặt đất thì máy bay đã dịch chuyển thêm 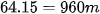 so với vị trí bắt đầu cất cánh, tức là cách gốc tọa độ là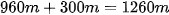
Kết luận: Vậy sau 15 giây cất cánh, phi cơ đang ở vị trí có tọa độ là .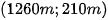

Câu 5: Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với tốc độ là 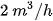 vào một cái bể đã chứa sẵn  nước.
a. Viết biểu thức tính thể tích y của nước có trong bể sau x giờ.
b. Gọi ∆ là đồ thị của hàm y=f(x) được xác định từ câu a. Viết phương trình tham số và phương trình tổng quát
của đường thẳng ∆ .

Lời giải

a. Vì sau mỗi giờ vòi chảy vào bể được 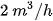, suy ra sau x giờ vòi chảy được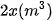
Vì trong bể đã chứa sẵn 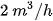 nước nên biểu thức tính thể tích y của nước có trong bể sau x giờ
là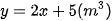
b. Đường thẳng ∆ là đồ thị của hàm số (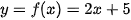, suy ra phương trình tổng quát của đường thẳng ∆ là 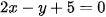. Đường thẳng ∆ có một vecto pháp tuyến  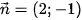nên có một vecto chỉ phương 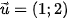. Hơn nữa đường thẳng ∆ đi qua điểm M(1; 7) nên có phương trình tham số là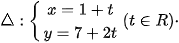

Câu 6: Có một công viên nhỏ hình tam giác như Hình 1. Người ta dự định đặt một cây đèn để chiếu sáng toàn bộ công viên. Để công việc tiến hành thuận lợi, người ta đo đạc và mô phỏng các kích thước công viên như Hình 2. Thiết lập một hệ trục Oxy như Hình 3, khi đó các đỉnh của công viên có tọa độ lần lượt là 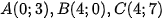. Gọi I là điểm đặt cây đèn sao cho đèn chiếu sáng toàn bộ công viên. Vậy cần đặt I ở vị trí có tọa độ bao nhiêu?

Lời giải

- Vùng mà cây đèn chiếu sáng được biểu diễn bằng một hình tròn mà điểm đặt cây đèn là tâm nên để chiếu sáng toàn bộ công viên ta cần đặt cây đèn ở tâm đường tròn ngoại tiếp tam giác.
- Gọi I(x;y) là tâm đường tròn ngoại tiếp tam giác .

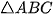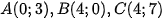Ta có: nên: 

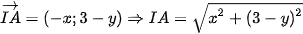
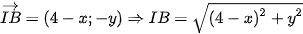
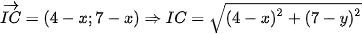
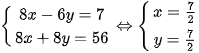Do I là tâm đường tròn ngoại tiếp tam giác ABC∆ nên ta có IA=IB=IC, ta lập được hệ phương trình .Vậy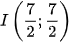

Câu 7: Khúc cua của một con đường có hình dạng parabol, điểm đầu vào khúc cua là A , điểm cuối là B , khoảng cách AB=400m. Đỉnh parabol (P) của khúc cua cách đường thẳng AB một khoảng 20m và cách đều A, B (tham khảo hình ảnh bên).

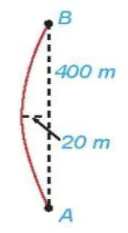
Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng tọa độ tương ứng với 1m trên thực tế.

Lời giải

Trong mặt phẳng tọa độ Oxy , với 1 đơn vị đo trong mặt phẳng tọa độ tương ứng với 1 m trên thực tế. Gọi phương trình chính tắc của parabol (P) là 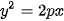 , với p>0 là tham số tiêu.

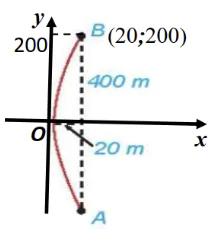
Từ hình vẽ, ta suy ra parabol (P) đi qua điểm B(20;200) , khi đó ta có phương trình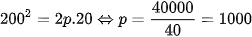

Kết luận: Vậy phương trình chính tắc của (P) là 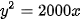.