Giải bài tập Bài 5 trang 49 Chuyên đề Toán 11 | Chuyên đề học tập Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 5 trang 49 Chuyên đề Toán 11. Bài 2. Một vài ứng dụng của lí thuyết đồ thị. Chuyên đề học tập Cánh diều
Đề bài:
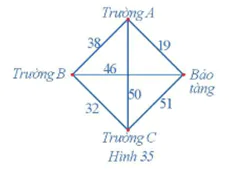
Một nhân viên của bảo tàng nghệ thuật đang có kế hoạch giới thiệu nội dung cuộc triển lãm của bảo tàng đến ba trường học trong khu vực. Người đó muốn đến từng trường và quay trở lại bảo tàng sau khi thăm cả ba trường. Thời gian di chuyển (đơn vị: phút) giữa các trường học và giữa bảo tàng với mỗi trường học được mô tả trong Hình 35.
Tìm chu trình xuất phát từ viện bảo tàng sao cho thời gian đi là ít nhất.
Đáp án và cách giải chi tiết:
Từ viện bảo tàng, thời gian di chuyển đến trường A là ngắn nhất: 19 phút.
Từ trường A, thời gian di chuyển đến trường B là ngắn nhất: 38 phút.
Từ trường B, thời gian di chuyển đến trường C là ngắn nhất: 32 phút.
Đến đây, không còn địa điểm nào chưa đi qua nên quay lại viện bảo tàng với thời gian di chuyển: 51 phút.
Do đó, chu trình xuất phát từ viện bảo tàng, qua trường A, trường B, trường C rồi quay lại viện bảo tàng có thời gian đi là ít nhất và thời gian đi là: 19 + 38 + 32 + 51 = 140 (phút).
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 44 Chuyên đề Toán 11
Như chúng ta đã biết, Lí thuyết đồ thị ra đời trong quá trình khái quát, mô phỏng những vấn đề của khoa học và thực tiễn thành những mô hình toán học. Vì thế, các kết quả của Lí thuyết đồ thị có nhiều ứng dụng trong khoa học và thực tiễn.
Lí thuyết đồ thị có thể giải quyết những vấn đề thực tiễn nào?
Hoạt động 1 trang 44 Chuyên đề Toán 11
Giả sử ba địa điểm A, B, C được nối với nhau theo những con đường AB, BC, CA với độ dài lần lượt là 15 km, 20 km, 16 km. Sử dụng đồ thị để mô tả tình huống đó.
Hoạt động 2 trang 44 Chuyên đề Toán 11
Giả sử có sáu địa điểm A, B, C, D, E, F được nối với nhau theo những con đường với độ dài (đơn vị: kilômét) được mô tả bằng đồ thị có trọng số ở Hình 24. Người giao hàng cần đi giao hàng tại sáu địa điểm trên. Người giao hàng xuất phát từ một địa điểm nào đó, đi qua các địa điểm còn lại để giao hàng và trở về địa điểm ban đầu. Hãy tìm một đường đi thỏa mãn điều kiện trên cho người giao hàng sao cho quãng đường mà người giao hàng phải di chuyển là ngắn nhất.

Luyện tập 2 trang 46 Chuyên đề Toán 11
Sử dụng thuật toán láng giềng gần nhất để giải bài toán trong Hoạt động 2.
Luyện tập 3 trang 47 Chuyên đề Toán 11
Hexane C6H14 có năm đồng phân. Vẽ đồ thị tương ứng với năm đồng phân đó.
Bài 1 trang 49 Chuyên đề Toán 11
Hình 31 biểu diễn mạng lưới máy chủ và tốc độ truyền dữ liệu (đơn vị: Megabit/ giây, kí hiệu là Mbps) giữa một số thành phố. Vẽ một đồ thị sử dụng điểm, đường để biểu diễn mạng lưới đó.

Bài 2 trang 49 Chuyên đề Toán 11
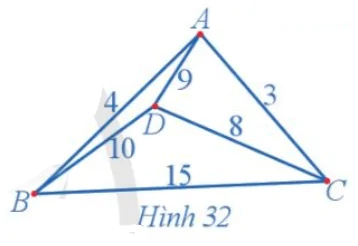
Có bốn địa điểm với độ dài quãng đường giữa các địa điểm (đơn vị: kilômét) mô tả trong Hình 32. Sử dụng thuật toán láng giềng gần nhất, tìm các chu trình xuất phát từ một đỉnh đi qua tất cả các địa điểm, mỗi địa điểm đúng một lần sao cho tổng độ dài các cạnh của chu trình là nhỏ nhất.
Bài 3 trang 49 Chuyên đề Toán 11
Giả sử chi phí di chuyển giữa các địa điểm được mô tả ở Hình 33 (đơn vị: nghìn đồng). Ta nên chọn theo chu trình nào đi qua tất cả các địa điểm để tổng chi phí di chuyển là thấp nhất? Chi phí thấp nhất đó bằng bao nhiêu?

Bài 4 trang 49 Chuyên đề Toán 11
Sử dụng thuật toán láng giềng gần nhất, hãy giải bài toán người giao hàng đối với đồ thị ở Hình 34, số ghi trên mỗi cạnh của đồ thị mô tả độ dài quãng đường giữa các địa điểm (đơn vị: kilômét).
