Tính bán kính mặt cầu ngoại tiếp khối đa diện dựa vào công thức tính nhanh và các phương pháp tính tổng quát khác | SBT Toán 12 - Chân trời sáng tạo (SBT)
Tính bán kính mặt cầu ngoại tiếp khối đa diện dựa vào công thức tính nhanh và các phương pháp tính tổng quát khác
Dưới đây là công thức Tính bán kính mặt cầu ngoại tiếp khối đa diện dựa vào công thức tính nhanh và các phương pháp tính tổng quát khác
A – CÁC PHƯƠNG PHÁP XÁC ĐỊNH TÂM MẶT CẦU NGOẠI TIẾP KHỐI ĐA DIỆN
Ta có hai cách thông thường để xác định tâm mặt cầu ngoại tiếp hình chóp như sau:
Cách 1:
Dựng trục ngoại tiếp Δ của đa giác đáy
Dựng mặt phẳng trung trực (P) của một cạnh bên
Giao của (P) và Δ là tâm mặt cầu ngoại tiếp I của hình chóp đã cho.
Cách 2:
Dựng trục ngoại tiếp Δ của đa giác đáy
Dựng trục ngoại tiếp d của đa giác mặt bên hoặc tam giác tạo thành từ ba đỉnh bất kì
Giao của Δ, d là tâm mặt cầu ngoại tiếp I của hình chóp đã cho.
Cách 3:
Dựng mặt phẳng trung trực (P) của một cạnh bên
Dựng mặt phẳng trung trực (Q) của một cạnh bên khác
Giao của (P) ∩ (Q) = Δ thì tâm mặt cầu nằm trên Δ.
Cách 4: Đặc biệt
Chỉ ra tất cả các điểm đều nhìn một đoạn thẳng dưới một góc vuông.
Tâm mặt cầu ngoại tiếp các điểm đó là trung điểm đoạn thẳng, bán kính.
ÁP DỤNG CHO KHỐI CHÓP BẤT KÌ
Xét hình chóp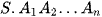 
có 
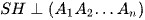và O là tâm ngoại tiếp đáy 
.
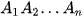Dựng đường thẳng qua O song song với SH, khi đó tâm mặt cầu ngoại tiếp I của hình chóp đã cho nằm trên đường thẳng này, gọi J là hình chiếu vuông góc của I lên SH.
Ta có IJHO là hình chữ nhật.
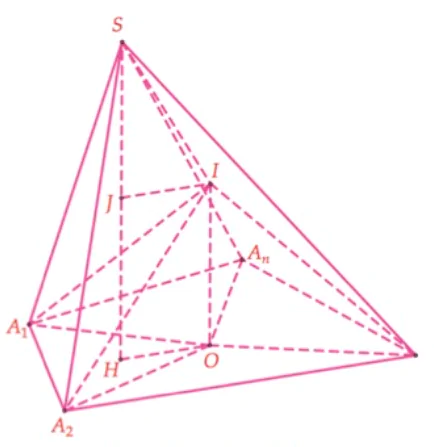
Đặt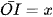 
, với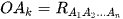 
, h = SH ta có
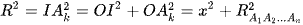và
.
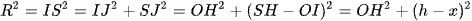So sánh hai đẳng thức trên, ta được: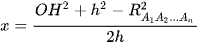 
.
Suy ra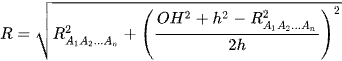 
.
*Chú ý: Tính độ dài OH bằng định lí hàm số côsin hoặc tính nhanh trong trường hợp đặc biệt.
x > 0 tương ứng S, I cùng phía so với mặt phẳng đáy; x < 0 tương ứng S, I khác phía so với mặt phẳng đáy.
Khối tứ diện gần đều ABCD đều AB = CA = a, AC = BD = b, AD = BC = c. Bán kính mặt cầu ngoại tiếp được tính theo công thức: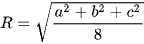 
.