Mẫu số liệu không ghép nhóm. Các số đặc trưng đo xu thế trung tâm và đo độ phân tán | Toán 10 - Cánh diều
Mẫu số liệu không ghép nhóm. Các số đặc trưng đo xu thế trung tâm và đo độ phân tán. Số trung bình, trung vị, tứ phân vị, mốt. Khoảng biến thiên, khoảng tứ phân vị, phương sai và độ lệch chuẩn
Dưới đây là công thức Mẫu số liệu không ghép nhóm. Các số đặc trưng đo xu thế trung tâm và đo độ phân tán
Dạng 1. Xác định số trung bình của mẫu số liệu
|
Số trung bình (số trung bình cộng) của mẫu số liệu
Trong trường hợp mẫu số liệu cho dưới dạng bảng tằn số thì số trung bình được tính theo công thức |
Ví dụ 1. Kết quả bốn lần kiểm tra môn toán của bạn Hoa là: 7,9,8,9 . Tính số trung bình cộng 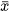 của mẫu số liệu trên.
của mẫu số liệu trên.
Lời giải.
Số trung bình cộng của mẫu số liệu trên là 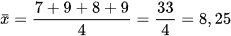
Số trung bình là giá trị trung bình cộng của các số trong mẫu số liệu, nó cho biết vị trí trung tâm của mẫu sổ liệu vì có thể dùng để đại diện cho mẫu số liệu.
Ví dụ 2. Thông kê số sách mô̄i bạn trong lớp đã đọc trong năm 2021, An thu được kêt quả như bảng bên. Hỏi trong năm 2021, trung bình mỗi bạn trong lớp đọc bao nhiêu cuốn sách?

Lời giải.
Số bạn trong lớp là n=3+5+15+10+7=40 (bạn).
Trong năm 2021, trung bình mỗi bạn trong lớp đọc số cuốn sách là 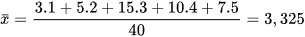 (cuốn)
(cuốn)
Dạng 2. Xác định số trung vị của mẫu số liệu
|
Để tìm trung vị
|
Ví dụ 1. Một công ty nhỏ gồm 1 giám đốc và 5 nhân viên, thu nhập mỗi tháng của giám đốc là 20 triệu đồng, của nhân viên là 4 triệu đồng. Tìm trung vị cho mẫu số liệu về lương của giám đốc và lương của nhân viên công ty.
Lời giải
Sắp xếp số liệu theo thứ tự không giảm 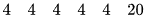
Dãy trên có hai giá trị chính giữa cùng bằng 4 . Vậy trung vị của mẫu số liệu cũng bằng 4 .
Lưu ý: Trung vị là giá trị chia đôi mẫu số liệu, nghĩa là trong mẫu số liệu đuợc sắp xếp theo thứ tự không giảm thì giá trị trung vị nằm ở vị trí chính giữa. Trung vị không bị ảnh hưởng bởi giá trị bất thường trong khi số trung bình bị ảnh hưởng bởi giá trị bất thường.
Ví dụ 2. Thời gian (tính theo phút) mà 10 người đợi ở bến xe buýt là
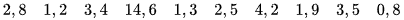
Tìm trung vị của mẫu số liệu trên.
Lời giải
Sắp xếp số liệu theo thứ tự không giảm
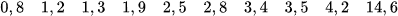
Dãy trên có hai giá trị chính giữa là 2,5 và 2,8 . Vî vậy 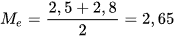 (phút).
(phút).
Dạng 3. Xác định tứ phân vị dựa vào mẫu số liệu
|
Để tìm các tứ phân vị của mấu xố liệu có n giá trị, ta làm như sau:
Khi đó, |
Ví dụ. Tìm tứ phân vị của mẫu số liệu sau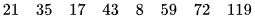
Lời giải.
Mẫu số liệu trên được sắp xếp theo thứ tự tăng dần
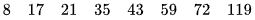
Trung vị của mẫu số liệu trên là 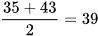 .
.
Trung vị của dãy 8, 17, 21, 35 là 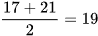 .
.
Trung vị của dãy 43, 59, 72, 119 là 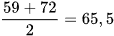 .
.
Vậy 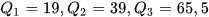 .
.
Tứ phân vị được biểu diển trên trục số như sau:

Dạng 4. Xác định Mốt mẫu số liệu
| Mốt của mẫu số liệu là giá trị xuất hiện với tần số lớn nhất. |
Ví dụ 1. Thời gian truy cập internet (đơn vị giờ) trong một ngày của một số học sinh lớp 10 được cho như sau
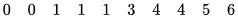
Tìm mốt của mẫu số liệu này.
Lời giải.
Vì số học sinh truy cập internet 1 giờ mỗi ngày là lớn nhất (có 3 học sinh) nên một là 1 .
Ví dụ 2. Số áo của một cửa hàng đã bán ra trong một tháng được thống kê trong bảng tần số sau Tìm mốt của mẫu số liệu này.
Tìm mốt của mẫu số liệu này.
Lời giải.
Vì tần số lớn nhất là 81 và 81 tương ứng với cỡ áo 40 nên mốt của bảng trên là 40 .
Dạng 5. Xác định khoảng biến thiên dựa vào mẫu số liệu
|
Khoảng biến thiên, kí hiệu là R, là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu. Khoảng biến thiên dùng để đo độ phân tán của mẫu số liệu. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán. |
Ví dụ. Điểm trung bình môn học kì của hai bạn An và Bình được cho bảng sau
a) Điểm trung bình môn học kì của hai bạn có như nhau không?
b) Tính các khoảng biến thiên của hai mẫu số liệu. Căn cứ trên mẫu số này, bạn nào học đồng đều hơn?
Lời giải.
a) Điểm trung bình môn học kì của An và Bình đều là 8,0 .
b) Đối với bạn An: Điểm trung bình môn thấp nhất, cao nhất tương ứng là 6,5; 9,5. Do đó khoảng biến thiên là 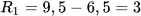 .
.
Đối với bạn Bình: Điểm trung bình môn thấp nhất, cao nhất tương ứng là 7,$6 ; 8,2$. Do đó khoảng biến thiên là  .
.
Do 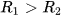 nên ta nói bạn Bình học đều hơn bạn An.
nên ta nói bạn Bình học đều hơn bạn An.
Dạng 6. Xác định khoảng tứ phân vị dựa vào mẫu số liệu
Khoảng tứ phân vị, kí hiệu là 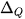 là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, tức là là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, tức là 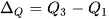 . .Một giá trị trong mẫu số liệu được coi là bất thường nếu nó nhỏ hơn 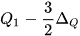 hoặc lớn hơn hoặc lớn hơn 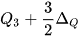 . Khoảng tứ phân vị cho ta cách nhận ra giá trị bất thường của mẫu số liệu. . Khoảng tứ phân vị cho ta cách nhận ra giá trị bất thường của mẫu số liệu. |
Ví dụ. Nêu các giá trị bất thường của mẫu số liệu thống kê sau
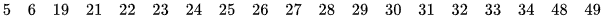
Lời giải.
Mẫu số liệu gồm 19 giá trị nên trung vị là số chính giữa 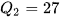 .
.
Nửa số liệu bên trái gồm 9 giá trị nên 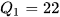 . Tương tự, nửa số liệu bên phải gồm 9 giá trị nên
. Tương tự, nửa số liệu bên phải gồm 9 giá trị nên 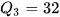 .
.
Suy ra 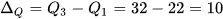 .
.
Các giá trị 5 ; 6 (nhỏ hơn 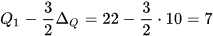 ) và các giá trị 48; 49 (lớn hơn
) và các giá trị 48; 49 (lớn hơn 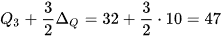 ) là các giá trị bất thường của mẫu số liệu.
) là các giá trị bất thường của mẫu số liệu.
Dạng 7. Xác định phương sai, độ lệch chuẩn dựa vào mẫu số liệu
Phương sai là giá trị 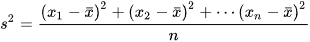 . .Căn bậc hai của phương sai 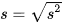 , được gọi là độ lệch chuẩn. , được gọi là độ lệch chuẩn. |
Ví dụ. Mẫu số liệu sau đây cho biết sĩ số của 5 lớp khối 10 tại một trường Trung học
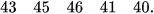
Tìm phương sai và độ lệch chuẩn cho mẫu số liệu này.
Lời giải.
Số trung bình của mẫu số liệu là 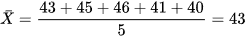 .
.
Ta có bảng sau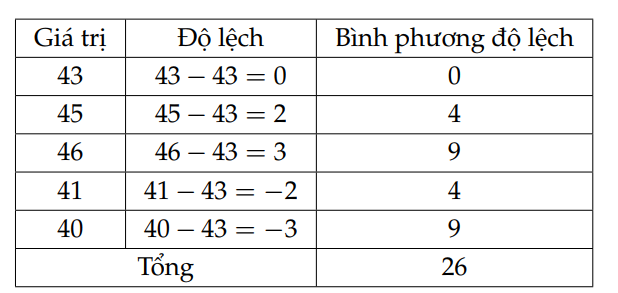
Mẫu số liệu trên gồm 5 giá trị nên 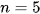 . Do đó phương sai là
. Do đó phương sai là 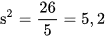 .
.
Độ lệnh chuẩn là 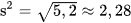 .
.
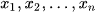 , kí hiệu là
, kí hiệu là 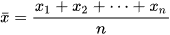
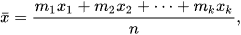
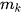 là tần số của giá trị
là tần số của giá trị 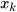 và
và 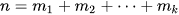 .
.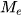 của một mẫu số liệu, ta thực hiện các bước sau:
của một mẫu số liệu, ta thực hiện các bước sau: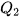 .
.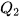 nếu n lẻ). Giá trị này là
nếu n lẻ). Giá trị này là 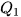 .
.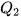 (không bao gồm
(không bao gồm 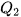 nếu n lẻ). Giá trị này là
nếu n lẻ). Giá trị này là 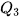 .
.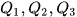 được gọi là các tứ phân vị của mẫu số liệu.
được gọi là các tứ phân vị của mẫu số liệu.