Mẫu số liệu ghép nhóm. Số trung bình; Mốt; Trung vị; Tứ phân vị; Phương sai và độ lệch chuẩn | Toán 11 - Chân trời sáng tạo
Số liệu ghép nhóm. Khoảng biến thiên. Số trung bình. Mốt. Trung vị. Tứ phân vị. Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm. Lớp 11 và 12.
Dưới đây là công thức Mẫu số liệu ghép nhóm. Số trung bình; Mốt; Trung vị; Tứ phân vị; Phương sai và độ lệch chuẩn
I. Số liệu ghép nhóm.
Mẫu số liệu ghép nhóm thường được trình bày dưới dạng bảng thống kê có dạng như sau:
Bảng 1: Bảng tần số ghép nhóm

- Bảng trên gồm k nhóm
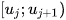 với
với 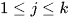 , mỗi nhóm gồm một số giá trị được ghép theo một tiêu chí xác định.
, mỗi nhóm gồm một số giá trị được ghép theo một tiêu chí xác định. - Cỡ mẫu
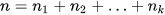 .
. - Giá trị chính giữa mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm
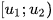 có giá trị đại diện là
có giá trị đại diện là 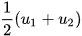 .
. - Hiệu
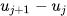 được gọi là độ dài của nhóm
được gọi là độ dài của nhóm  .
. - Khoảng biến thiên của mẫu số liệu ghép nhóm là
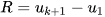 . Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán. Tuy nhiên, trong một số trường hợp
. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán. Tuy nhiên, trong một số trường hợp 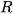 không phản ánh được mức độ phân tán của mẫu số liệu ghép nhóm.
không phản ánh được mức độ phân tán của mẫu số liệu ghép nhóm.
Một số quy tắc ghép nhóm của mẫu số liệu:
Mỗi mẫu số liệu có thể được ghép nhóm theo nhiều cách khác nhau nhưng thường tuân theo một số quy tắc sau:
- Sử dụng từ
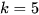 đến
đến 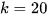 nhóm. Cỡ mẫu càng lớn thì cần càng nhiều nhóm số liệu. Các nhóm có cùng độ dài bằng L thoả mãn
nhóm. Cỡ mẫu càng lớn thì cần càng nhiều nhóm số liệu. Các nhóm có cùng độ dài bằng L thoả mãn 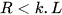 , trong đó R là khoảng biến thiên, k là số nhóm.
, trong đó R là khoảng biến thiên, k là số nhóm. - Giá trị nhỏ nhất của mẫu thuộc vào nhóm
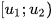 và càng gần
và càng gần 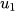 càng tốt. Giá trị lớn nhất của mẫu thuộc nhóm
càng tốt. Giá trị lớn nhất của mẫu thuộc nhóm 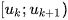 và càng gần
và càng gần 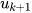 càng tốt.
càng tốt.
II. Số trung bình.
Giả sử mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm:
 Số trung bình của mẫu số liệu ghép nhóm, kí hiệu
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu 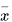 , được tính như sau:
, được tính như sau:
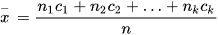
trong đó 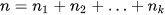 .
.
Ý nghĩa của số trung bình của mẫu số liệu ghép nhóm
Số trung bình của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho số trung bình của mẫu số liệu gốc. Nó thường dùng để đo xu thế trung tâm của mẫu số liệu.
III. Mốt.
Nhóm chứa mốt của mẫu số liệu ghép nhóm là nhóm có tần số lớn nhất.
Giả sử nhóm chứa mốt là 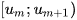 , khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là
, khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là 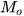 , được xác định bởi công thức
, được xác định bởi công thức
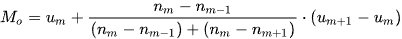 Chú ý: Nếu không có nhóm kề trước của nhóm chứa mốt thì
Chú ý: Nếu không có nhóm kề trước của nhóm chứa mốt thì 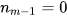 . Nếu không có nhóm kề sau của nhóm chứa mốt thì
. Nếu không có nhóm kề sau của nhóm chứa mốt thì 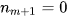 .
.
- Ýnghĩa của mốt của mẫu số liệu ghép nhóm
- Mốt của mẫu số liệu không ghép nhóm là giá trị có khả năng xuất hiện cao nhất khi lấy mẫu. Mốt của mẫu số liệu sau khi ghép nhóm
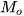 xấp xỉ với mốt của mẫu số liệu không ghép nhóm. Các giá trị nằm xung quanh
xấp xỉ với mốt của mẫu số liệu không ghép nhóm. Các giá trị nằm xung quanh 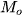 thường có khả năng xuất hiện cao hơn các giá trị khác.
thường có khả năng xuất hiện cao hơn các giá trị khác. - Một mẫu số liệu ghép nhóm có thể có nhiều nhóm chứa mốt và nhiều mốt.
Lưu ý
- Các đầu mút của các nhóm có thể không là giá trị của mẫu số liệu.
- Ta hay gặp các bảng số liệu ghép nhóm là số nguyên, chẳng hạn như bảng thống kê số lỗi chính tả trong bài kiểm tra giữa học kì 1 môn Ngữ Văn của học sinh khối 11 như sau:

Bảng số liệu này không có dạng như trên
Để thuận lợi cho việc tính các số đặc trưng cho bảng số liệu này, người ta hiệu chỉnh về dạng như bảng sau bằng cách thêm và bớt 0,5 đơn vị vào đầu mút bên phải và bên trái của mỗi nhóm số liệu như sau:

IV. Trung vị.
- Trong trường hợp mẫu số liệu có giá trị bất thường ( rất lớn hoặc rất bé so với đa số các giá trị khác), người ta không dùng số trung bình để đo xu thế trung tâm mà dùng trung vị.
- Trung vị
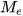 là giá trị chia đôi mẫu số liệu, nghĩa là trong mẫu số liệu được sắp xếp theo thứ tự không giảm thì giá trị trung vị ở vị trí chính giữa.
là giá trị chia đôi mẫu số liệu, nghĩa là trong mẫu số liệu được sắp xếp theo thứ tự không giảm thì giá trị trung vị ở vị trí chính giữa.
Công thức xác định trung vị của mẫu số liệu ghép nhóm:
- Gọi n là cỡ mẫu.
- Giả sử nhóm
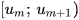 chứa trung vị;
chứa trung vị; 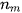 là tần số của nhóm chứa trung vị;
là tần số của nhóm chứa trung vị;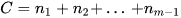 .
.
Khi đó
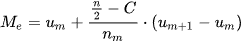
Ý nghĩa của trung vị của mẫu số liệu ghép nhóm
- Từ dữ liệu ghép nhóm nói chung không thể xác định chính xác trung vị của mẫu số liệu gốc. Trung vị của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho mẫu số liệu gốc và có thể lấy làm giá trị đại diện cho mẫu số liệu.
V. Tứ phân vị.
1. Công thức xác định tứ phân vị của mẫu số liệu ghép nhóm
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm, kí hiệu 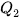 , cũng chính là trung vị
, cũng chính là trung vị 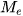 của mẫu số liệu ghép nhóm.
của mẫu số liệu ghép nhóm.
Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu 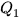 , ta thực hiện như sau:
, ta thực hiện như sau:
- Giả sử nhóm
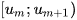 chứa tứ phân vị thứ nhất;
chứa tứ phân vị thứ nhất; 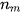 là tần số của nhóm chứa tứ phân vị thứ nhất;
là tần số của nhóm chứa tứ phân vị thứ nhất;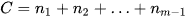
Khi đó:
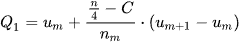
Tương tự, để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu 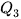 , ta thực hiện như sau:
, ta thực hiện như sau:
- Giả sử nhóm
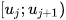 chứa tứ phân vị thứ ba;
chứa tứ phân vị thứ ba; 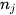 là tần số của nhóm chứa tứ phân vị thứ ba;
là tần số của nhóm chứa tứ phân vị thứ ba;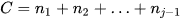
Khi đó:
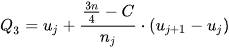
Ý nghĩa của tứ phân vị của mẫu số liệu ghép nhóm
- Ba điểm tứ phân vị chia mẫu số liệu đã sắp xếp theo thứ tự không giảm thành bốn phần đều nhau. Giống như với trung vị, nói chung không thể xác định chính xác các điểm tứ phân vị của mẫu số liệu ghép nhóm.
- Bộ ba tứ phân vị của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho tứ phân vị của mẫu số liệu gốc và được sử dụng làm giá trị đo xu thế trung tâm của mẫu số liệu.
- Tứ phân vị thứ nhất và thứ ba đo xu thế trung tâm của nửa dưới (các dữ liệu nhỏ hơn
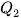 ) và nửa trên (các dũ liệu lớn hơn
) và nửa trên (các dũ liệu lớn hơn 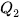 ) của mẫu số liệu.
) của mẫu số liệu.
2. Khoảng tứ phân vị
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu 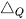 , là hiệu giữa tứ phân vị thứ ba
, là hiệu giữa tứ phân vị thứ ba 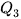 và tứ phân vị thứ nhất
và tứ phân vị thứ nhất 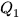 của mẫu số liệu ghép nhóm đó, tức là:
của mẫu số liệu ghép nhóm đó, tức là: 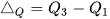 .
.
Ý nghĩa của khoảng tứ phân vị của mẫu số liệu ghép nhóm
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho khoảng tứ phân vị của mẫu số liệu gốc và có thể dùng để đo mức độ phân tán của nửa giữa của mẫu số liệu (tập hợp gồm 50% số liệu nằm chính giữa mẫu số liệu).
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm càng nhỏ thì dữ liệu càng tập trung xung quanh trung vị.
- Khoảng tứ phân vị được dùng để xác định giá trị bất thường (giá trị ngoại lệ) trong mẫu số liệu. Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu
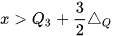 hoặc
hoặc 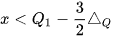 .
. - Khoảng tứ phân vị của mẫu số liệu ghép nhóm không bị ảnh hưởng nhiều bởi các giá trị bất thường (giá trị ngoại lệ) trong mẫu số liệu.
VI. Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm.
Phương sai của mẫu số liệu ghép nhóm kí hiệu 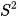 , được tính bởi công thức:
, được tính bởi công thức:
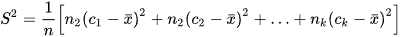
trong đó: 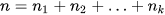 là cỡ mẫu; và
là cỡ mẫu; và 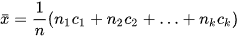 là số trung bình.
là số trung bình.
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu 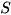 , là căn bậc hai số học của phương sai, nghĩa là
, là căn bậc hai số học của phương sai, nghĩa là 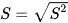 .
.
Chú ý:
a) Phương sai của mẫu sổ liệu ghép nhóm có thể được tính theo công thức sau:
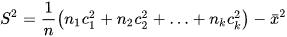
b) Trong thống kê, người ta còn đùng đại lượng sau để đo mức độ phân tán cưa mẫu số liệu ghép nhóm:
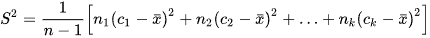
Ý nghĩa của phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm
- Phương sai của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho phương sai của mẫu số liệu gốc.
- Độ lệch chuẩn của mẫu số liệu ghép nhóm cũng là giá trị xấp xỉ cho độ lệch chuẩn của mẫu số liệu gốc. Chúng được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm. Phương sai và độ lệch chuẩn càng lớn thì dữ liệu càng phân tán.
- Độ lệch chuẩn có cùng đơn vị với đơn vị của mẫu số liệu.
Một số bài tập ứng dụng công thức Mẫu số liệu ghép nhóm. Số trung bình; Mốt; Trung vị; Tứ phân vị; Phương sai và độ lệch chuẩn:
Bài 3.1 trang 61 Toán 11 Tập 1
Trong các mẫu số liệu sau, mẫu nào là mẫu số liệu ghép nhóm? Đọc và giải thích mẫu số liệu ghép nhóm đó.
a) Số tiền mà sinh viên chi cho thanh toán cước điện thoại trong tháng.

b) Thống kê nhiệt độ tại một địa điểm trong 40 ngày, ta có bảng số liệu sau:

Bài 3.2 trang 61 Toán 11 Tập 1
Số sản phẩm một công nhân làm được trong một ngày được cho như sau:

Hãy chuyển mẫu số liệu sang dạng ghép nhóm với sáu nhóm có độ dài bằng nhau.
Bài 3.3 trang 61 Toán 11 Tập 1
Thời gian ra sân (giờ) của một số cựu cầu thủ ở giải ngoại hạng Anh qua các thời kì được cho như sau:

Hãy chuyển mẫu số liệu trên sang dạng ghép nhóm với bảy nhóm có độ dài bằng nhau.
Bài 3.4 trang 67 Toán 11 Tập 1
Quãng đường (km) đi từ nhà đến nơi làm việc của 40 công nhân một nhà máy được ghi lại như sau:

a) Ghép nhóm dãy số liệu trên thành các khoảng có độ rộng bằng nhau, khoảng đầu tiên là [0; 5). Tìm giá trị đại diện cho mỗi nhóm.
b) Tính số trung bình của mẫu số liệu không ghép nhóm và mẫu số liệu ghép nhóm. Giá trị nào chính xác hơn?
c) Xác định nhóm chứa mốt của mẫu số liệu ghép nhóm thu được.
Bài 3.5 trang 67 Toán 11 Tập 1
Tuổi thọ (năm) của 50 bình ắc quy ô tô được cho như sau:
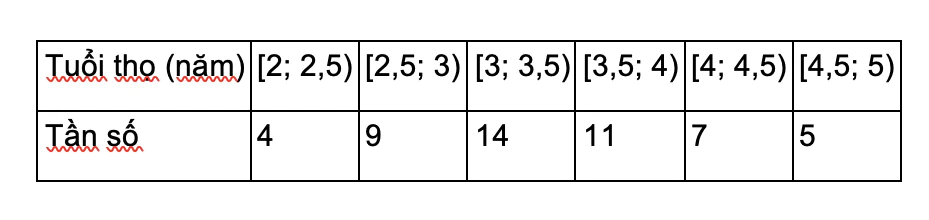
a) Xác định mốt và giải thích ý nghĩa.
b) Tính tuổi thọ trung bình của 50 bình ắc quy ô tô này.
Bài 3.6 trang 67 Toán 11 Tập 1
Điểm thi môn Toán (thang điểm 100, điểm được làm tròn đến 1) của 60 thí sinh được cho trong bảng sau:

a) Hiệu chỉnh để thu được mẫu số liệu ghép nhóm dạng Bảng 3.2.
b) Tìm các tứ phân vị và giải thích ý nghĩa của chúng.
Bài 3.7 trang 67 Toán 11 Tập 1
Phỏng vấn một số học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối, thu được bảng số liệu ở bên.
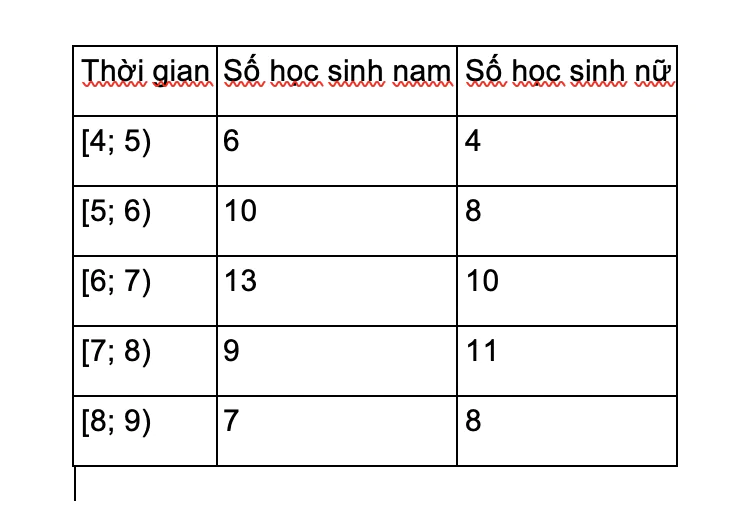
a) So sánh thời gian ngủ trung bình của các bạn học sinh nam và nữ.
b) Hãy cho biết 75% học sinh khối 11 ngủ ít nhất bao nhiêu giờ?
Bài 3.8 trang 69 Toán 11 Tập 1
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Giá trị đại diện của nhóm [20; 40) là
A. 10.
B. 20.
C. 30.
D. 40.
Bài 3.9 trang 69 Toán 11 Tập 1
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
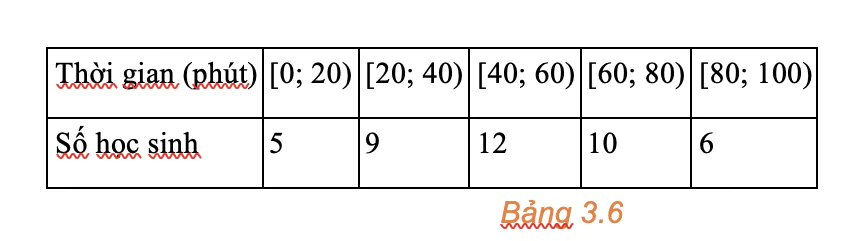
Mẫu số liệu ghép nhóm này có số mốt là
A. 0.
B. 1.
C. 2.
D. 3.
Bài 3.10 trang 69 Toán 11 Tập 1
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
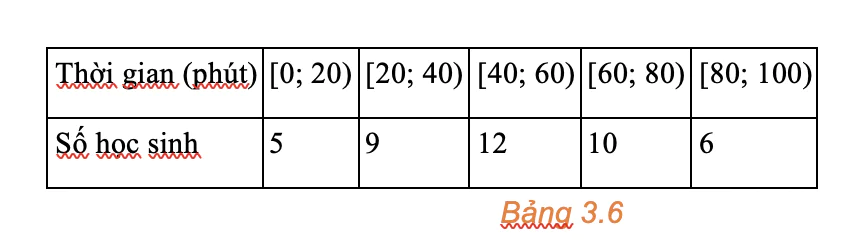
Nhóm chứa mốt của mẫu số liệu này là
A. [20; 40).
B. [40; 60).
C. [60; 80).
D. [80; 100).