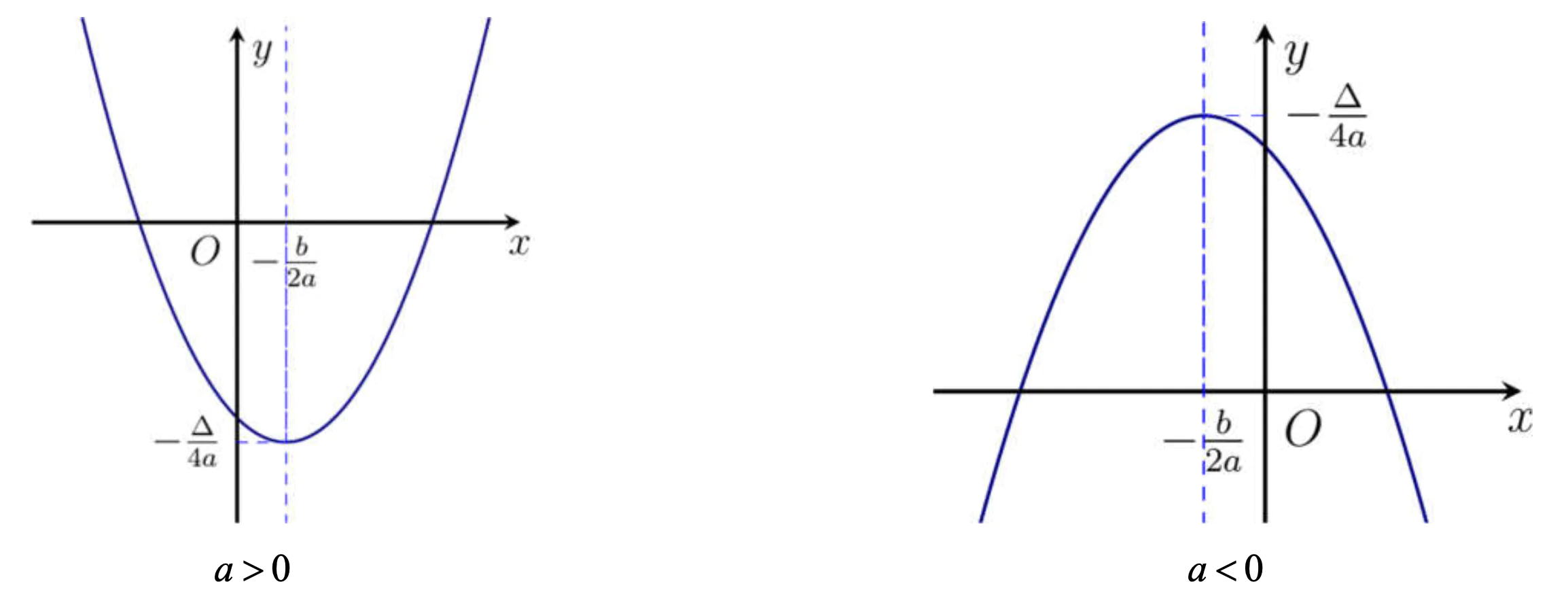Hàm số bậc hai | Toán 10 - Cánh diều
Hàm số bậc hai
Dưới đây là công thức Hàm số bậc hai
1. Định nghĩa
Hàm số bậc hai là hàm số được cho bởi công thức y = f(x) =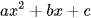 
. Trong đó 
và 
.
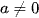- Tập xác định D =
. - Đỉnh I
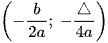với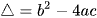 
.
- Trục đối xứng là đường x =
.
2. Sự biến thiên
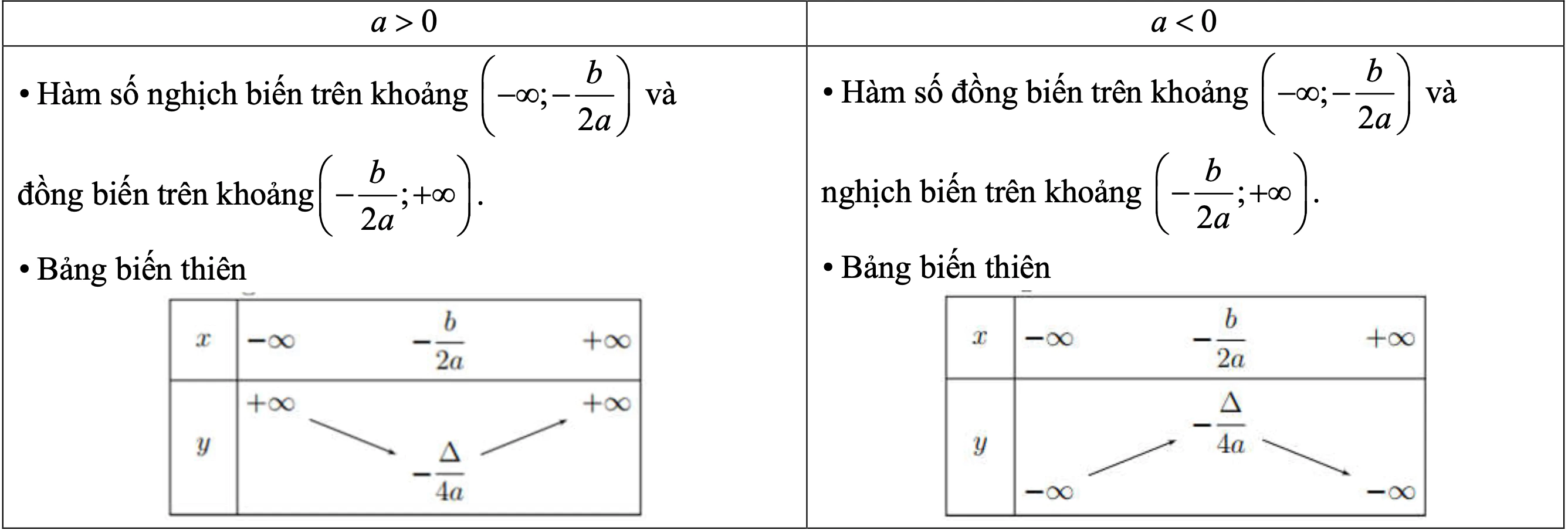
3. Cách vẽ đồ thị
Đồ thị hàm số bậc hai là đường parabol. Để vẽ đồ thị hàm số bậc hai ta thực hiện các bước
a) Xác định tọa độ đỉnh I.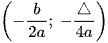
b) Vẽ trục đối xứng x = .
c) Xác định tọa độ giao điểm của parabol với trục tung và trục hoành (nếu có).
d) Căn cứ vào tính đối xứng, bề lõm và hình dạng parabol để nối các điểm đó lại.
