GIỚI HẠN HÀM SỐ | Toán 11 - Kết nối tri thức
GIỚI HẠN HÀM SỐ
Dưới đây là công thức GIỚI HẠN HÀM SỐ
GIỚI HẠN HÀM SỐ
Các dạng vô định: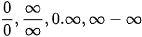 
.
Khi làm bài BẮT BUỘC phải kiểm tra có dạng vô định trước khi áp dụng phương pháp bên dưới .
1. Dạng vô định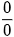 
Tính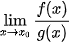 
khi 
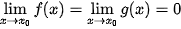, trong đó f(x),g(x) là các đa thức hoặc căn thức.
Phương pháp:
Bước 1: Phân tích tử và mẫu thành tích các nhân tử.
Bước 2: Chia cả tử và mẫu cho nhân tử chung của tử và mẫu.
Bước 3: Tính giới hạn theo cách thông thường.
Nếu f(x) và g(x) có chứa căn thức thì có thể nhân lượng liên hợp
Ví dụ:
.
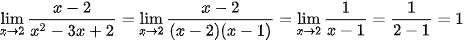
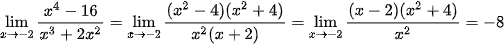
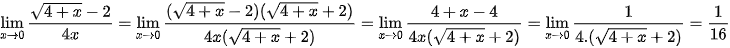2. Dạng vô định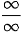 
Tính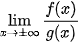 
khi 
, trong đó f(x),g(x) là các đa thức.
Phương pháp.
Bước 1: Đặt lũy thừa bậc cao nhất của tử và mẫu ra làm nhân tư chung.
Bước 2: Chia cà tử và mẫu cho lũy thừa bậc cao nhất của x.
Bước 3: Tính các giới hạn thông thường và suy ra kết quả.
Ví dụ:
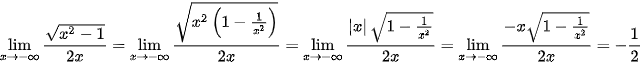
3. Dạng vô định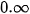 
Tính giới hạn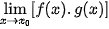 
khi 
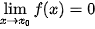và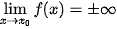 
Phương pháp:
Bước 1: Biến đổi 
để đưa về dạng 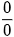hoặc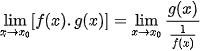 
để đưa về dạng .
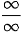Bước 2: Sử dụng các phương pháp của dạng 1 và 2 đề tính tiếp giới hạn.
4. Dạng vô định 
Tính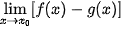 
khi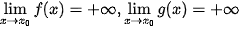 
hoặc tính 
khi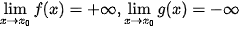 
.
Phương pháp:
Bước 1: Nhân hoặc chia với biểu thức liên hợp (căn thức) hoặc quy đồng đề đưa về cùng một phân thức.
Bước 2: Thực hiện tính giới hạn dựa theo các dạng đã biết.
Ví dụ:
