Dãy số tăng, dãy số giảm và dãy số bị chặn | Toán 11 - Cánh diều
Dãy số tăng, dãy số giảm và dãy số bị chặn
Dưới đây là công thức Dãy số tăng, dãy số giảm và dãy số bị chặn
I. ĐỊNH NGHĨA
1. Định nghĩa dãy số
Mỗi hàm số u xác định trên tập các số nguyên dương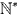 
được gọi là một dãy số vô hạn (gọi tắt là dãy số).
Kí hiệu:
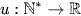
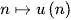
Người ta thường viết dãy số dưới dạng khai triển
trong đó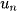 
= u(n) hoặc viết tắt là 
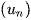, và gọi 
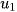là số hạng đầu, 
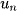là số hạng thứ n và là số hạng tổng quát của dãy số.
Ví dụ: Dãy số tự nhiên lẻ 1, 3, 5, 7,... có số hạng đầu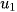 
= 1 và số hạng tổng quát 
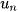= 2n - 1.
2. Định nghĩa dãy số hữu hạn
Mỗi hàm số u xác định trên tập M = {1; 2; 3; ...; m} với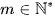 
được gọi là một dãy số hữu hạn.
Dạng khai triển của nó là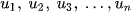 
, trong đó 
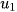là số hạng đầu, 
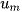là số hạng cuối.
Ví dụ: Dãy số -1, 0, 1, 2, 3, 4 là dãy số hữu hạn có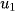 
= -1 và 
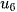= 4.
II. CÁCH CHO MỘT DÃY SỐ
1. Dãy số cho bằng công thức của số hạng tổng quát
Ví dụ: Cho dãy số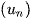 
với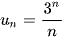 
.
2. Dãy số cho bằng phương pháp mô tả
3. Dãy số cho bằng phương pháp truy hồi
Cách cho một dãy số bằng phương pháp truy hồi, tức là:
a) Cho số hạng đầu (hay vài số hạng đầu).
b) Cho hệ thức truy hồi, tức là hệ thức biểu thị số hạng thứ n qua số hạng (hay vài số hạng) đứng trước nó.
Ví dụ: Dãy Fibonacci là dãy số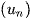 
được xác định như sau: 
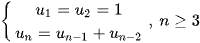. Nghĩa là kể từ số hạng thứ 3 trở đi, mỗi số hạng đều bằng tổng của hai số hạng đứng ngay trước nó.
III. DÃY SỐ TĂNG, GIẢM VÀ BỊ CHẶN
1. Dãy số tăng, dãy số giảm
Dãy số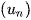 
được gọi là dãy số tăng nếu 
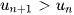với mọi 
.
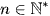Dãy số 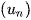được gọi là dãy số tăng nếu 
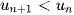với mọi .
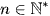Chú ý: Không phải mọi dãy số đều tăng hoặc giảm. Chẳng hạn, dãy số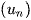 
với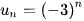 
tức là dãy -3; 9; -27; 81; ... không tăng cũng không giảm.
Phương pháp giải.
Cách 1: Xét hiệu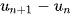 
.
- Nếu
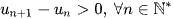thì 
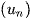là dãy số tăng. - Nếu
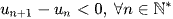thì 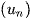là dãy số giảm.
Cách 2: Khi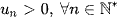 
ta xét tỉ số 
.
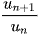- Nếu
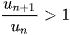thì 
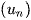là dãy số tăng. - Nếu
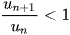thì 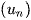là dãy số giảm.
Cách 3: Nếu dãy số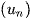 
được cho bởi một hệ thức truy hồi thì ta có thể sử dụng phương pháp quy nạp để chứng minh 
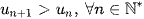(hoặc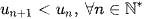 
).
* Công thức giải nhanh một số dạng toán về dãy số
Dãy s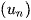ố 
có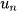 
= an + b tăng khi a > 0 và giảm khi a < 0.
Dãy số 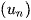có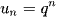 
-
Không tăng, không giảm khi q < 0.
-
Giảm khi 0 < q < 1.
-
Tăng khi q > 1.
Dãy s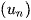ố có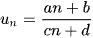 
với điều kiện cn + d > 0, 
.
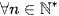- Tăng khi ad - bc > 0.
- Giảm khi ad - bc < 0.
Dãy số đan dấu cũng là dãy số không tăng, không giảm. Ví dụ -1; 1; -1; 1; ...
2. Dãy số bị chặn
Dãy số 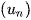được gọi là bị chặn trên nếu tồn tại một số M sao cho
.
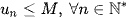Dãy số 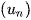được gọi là bị chặn dưới nếu tồn tại một số m sao cho
.
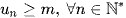Dãy số 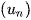được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho
.
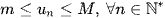Lưu ý:
+ Dãy tăng sẽ bị chặn dưới bởi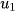 
.
+ Dãy giảm sẽ bị chặn trên bởi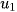 
.
A. Phương pháp giải
Phương pháp 1: Chứng minh trực tiếp bằng các phương pháp chứng minh bất đẳng thức
Dãy s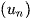ố 
có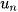 
= f(n) là hàm số đơn giản.
Ta chứng minh trực tiếp bất đẳng thứ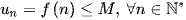c 
hoặc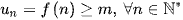 
.
Chú ý: Nếu dãy số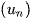 
giảm thì bị chặn trên, dãy số 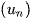tăng thì bị chặn dưới.
* Công thức giải nhanh một số dạng toán về dãy số bị chặn
Dãy số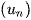 
có 
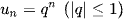bị chặn
Dãy s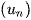ố có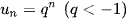 
không bị chặn
Dãy s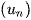ố có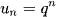 
với q > 1 bị chặn dưới
Dãy s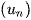ố có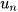 
= an + b bị chặn dưới nếu a > 0 và bị chặn trên nếu a < 0
Dãy số 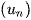có 
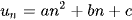bị chặn dưới nếu a > 0 và bị chặn trên nếu a < 0
Dãy s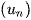ố có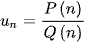 
trong đó P(n) và Q(n) là các đa thức, bị chặn nếu bậc của P(n) nhỏ hơn hoặc bằng bậc của Q(n)
Dãy s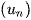ố có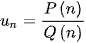 
trong đó P(n) và Q(n) là các đa thức, bị chặn dưới hoặc bị chặn trên nếu bậc của P(n) lớn hơn bậc của Q(n)