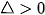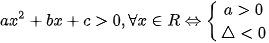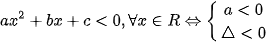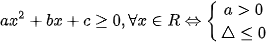DẤU CỦA TAM THỨC BẬC HAI | Toán 10 - Cánh diều
DẤU CỦA TAM THỨC BẬC HAI
Dưới đây là công thức DẤU CỦA TAM THỨC BẬC HAI
I. LÝ THUYẾT TRỌNG TÂM
1.Định nghĩa
-Tam thức bậc hai (đối với x ) là biểu thức dạng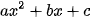 
. Trong đó a, b, c là những số cho trước với 
.
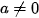-Nghiệm của phương trình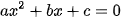 
được gọi là ngiệm của tam thức bậc hai.
- 
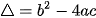và 
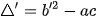theo thứ tự được gọi là biệt thức và biệt thức thu gọn của tam thức bậc hai.
2. Dấu của tam thức bậc hai
Dấu của tam thức bậc hai được thể hiện trong bảng sau
 |
|||
 |
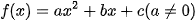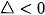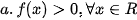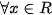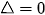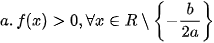 hay f(X) cùng dấu với a,  |
||
 |
 hay f(X) cùng dấu với a,  |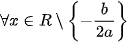
||
|
(trong trái ngoài cùng) |
    |
||
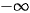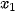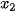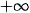| cùng dấu với a 0 trái dấu với a 0 cùng dấu với a | |||
3. Nhận xét
Cho tam thực bậc hai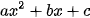 
, ta có các trường hợp sau
|
|
|
|
|
|
II. CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1. Dấu của tam thức bậc hai
Phương pháp: Dựa vào định lý về dấu của tam thức bậc hai.
Đối với đa thức bậc cao P(x) ta làm như sau:
1) Phân tích đa thức P(x) thành tích các tam thức bậc hai (hoặc có cả nhị thức bậc nhất).
2) Lập bảng xét dấu của P(x). Từ đó suy ra dấu của P(x).
Đối với phân thức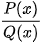 
(trong đó P(x), Q(x) là các đa thức) ta làm như sau
1) Phân tích đa thức P(x), Q(x) thành tích các tam thức bậc hai (hoặc có cả nhị thức bậc nhất).
2) Lập bảng xét dấu của P(x) và Q(x). Từ đó suy ra dấu của .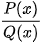
Ví dụ: Xét dấu của các tam thức sau
a)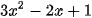 
b)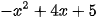 
.
Lời giải.
a) Ta có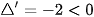 
và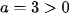 
. Suy ra 
.
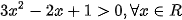b) Ta có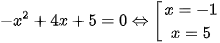 
.
Bảng xét dấu
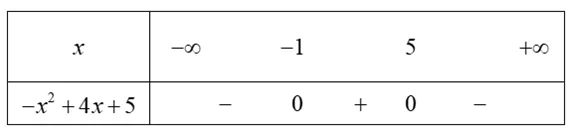
Suy r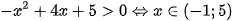a 
và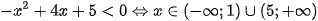 
.
Dạng 2. Bất phương trình bậc hai
1. Định nghĩa. Bất phương trình bậc hai (ẩn x) là bất phương trình có một trong các dạng f(x)>0, f(x)<0,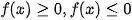 
, .
Trong đó f(x) là một tam thức bậc hai.
2. Cách giải. Để giải bất phương trình bậc hai, ta áp dụng định lí về dấu của tam thức bậc hai.
3. Ứng dụng. Giải bất phương trình tích, thương chứa các tam thức bậc hai bằng cách lập bảng xét dấu của chúng
Ví dụ: Giải các bất phương trình sau
a)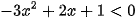 
b)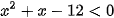 
Giải
a) Ta có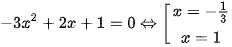 
Bảng xét dấu
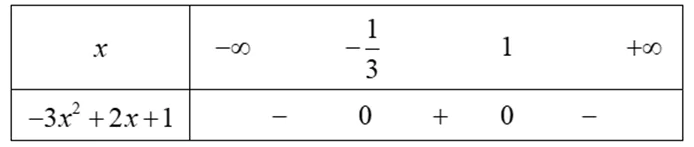
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình là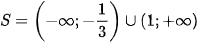 
b) Ta có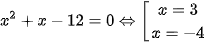 
Bảng xét dấu
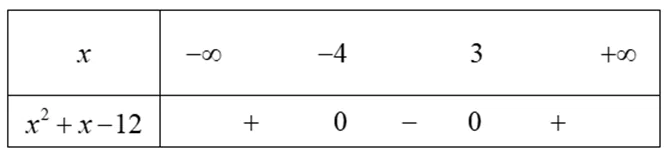
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình là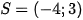 
Dạng 3. Bài toán tham số liên quan đến tam thức bậc hai
Ví dụ: Tìm để các phương trình sau có nghiệm.
a)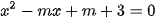 
b)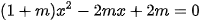 
Giải
a) Phương trình có nghiệm khi và chỉ khi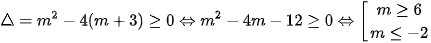 
Vậy với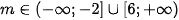 
thì phương trình có nghiệm.
b)
Với m=-1, phương trình trở thành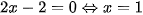 
. Suy ra m=-1 thỏa mãn yêu cầu bài toán.
Với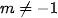 
phương trình có nghiệm khi và chỉ khi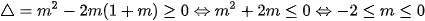 
Vậy với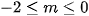 
thì phương trình có nghiệm.